Substitution
Falls, du nicht darauf gekommen bist, was man hier am besten substituiert, schau dir einfach die nächste Zeile an!
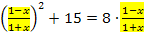
Wir schreiben also statt dem Bruch 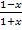 einfach u und erhalten dadurch direkt eine gemischtquadratische Gleichung mit der neuen Variablen u.
einfach u und erhalten dadurch direkt eine gemischtquadratische Gleichung mit der neuen Variablen u.
Subst.: 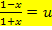
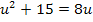
![]() |
| 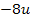
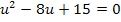
Das sieht doch gleich viel besser aus! Mit der Mitternachtsformel erhalten wir:
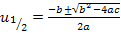
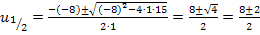
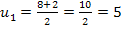
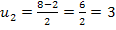
Zum Schluss wieder die Rücksubstitution:
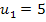 in
in 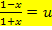

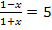
![]() |
| 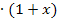
![]()
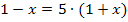
![]()
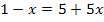 |
| 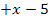
![]()
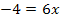
![]() |
| 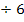
![]()
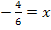
![]()
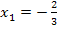
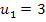 in
in 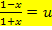

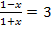
![]() |
| 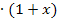
![]()
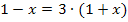
![]()
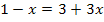 |
| 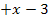
![]()
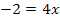
![]() |
| 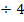
![]()
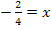
![]()
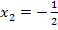
Beide Werte liegen innerhalb der Definitionsmenge D = ℝ 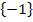 . Somit sind die gesuchten Lösungen
. Somit sind die gesuchten Lösungen 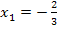 und
und 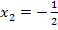 .
.
An diesen Aufgaben wurde es hoffentlich klar, dass eine geeignete Substitution die Rechnung deutlich erleichtern kann. Stell´dir vor, du hättest die letzte Aufgabe ohne Substitution zu lösen versucht. Au weia! Das wäre echt übel geworden. Tu dir das bitte nicht an und lerne lieber die Substitution! Wenn schon in der Aufgabenstellung steht, dass eine neue Variable eingeführt werden soll, also eine Substitution verwendet werden soll, ist das meist auch relativ gut zu erkennen, was man durch u ersetzen soll. Die Kunst ist es allerdings später in anderem Zusammenhang selbst darauf zu kommen, dass eine Substitution helfen kann. Das hat dann natürlich auch mit Erfahrung, sprich Übung zu tun. Substitutionen werden dir noch oft an verschiedensten Stellen begegnen. Mehr zur Substitution (ab 10. Klasse Gymnasium bzw. 12. Klasse FOS/BOS mathematischer Zweig) findest du unter anderem daher auch in den Kapiteln Gleichungen dritten und höheren Grades und Exponential- und Logarithmusgleichungen (Goniometrische Gleichungen).
Falls du dich noch nicht damit beschäftigt hast, wie man die Anzahl der Lösungen einer gemischtquadratischen Gleichung mit Hilfe der Diskriminante D ermittelt, ist es empfehlenswert, jetzt mit dem Kapitel Diskriminante D weiter zu machen.
Wenn du nun aber lieber lernen möchtest, wie gemischtquadratische Gleichungen mit Hilfe der quadratischen Ergänzung gelöst werden können, gehe zu:Quadratische Ergänzung (zur Lösung gemischtquadratischer Gleichungen)

