Substitution
zu b.)
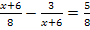
Als erstes stellen wir fest, dass hier eine Bruchgleichungvorliegt, denn x kommt im Nenner vor. Daher überlegen wir uns vorweg die Definitionsmenge. (Auch wenn es gar nicht extra gefragt ist, muss das gemacht werden!) Was darf hier für x überhaupt eingesetzt werden? Da der Nenner nicht Null ergeben darf, kann für x nicht -6 eingesetzt werden, denn sonst wird der Nenner des zweiten Bruchs auf der linken Seite der Gleichung Null. Es gilt also:
D = ℝ 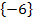
Jetzt müssen wir die Gleichung mittels Substitution nach x auflösen. So, was soll man den bei dieser Gleichung nun gleich u setzen? Eigentlich wollen wir durch die Substitution zu einer einfacheren Gleichung kommen. Das gelingt hier, indem man den Ausdruck x + 6 durch u ersetzt.
Subst.: 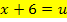
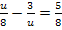
Bei dieser Gleichung handelt es sich immer noch um eine Bruchgleichung, aber nun mit der neuen Variablen u. Wir bringen beide Seiten der Gleichung auf einen gemeinsamen Nenner und multiplizieren danach mit dem Hauptnenner. (Stattdessen kannst du auch nur auf der linken Seite die beiden Brüche auf einen gemeinsamen Nenner bringen und danach „kreuzweise“ multiplizieren, wie im 8. Bsp. vorgeführt. Genaueres zu den verschiedenen Methoden, wie man Bruchgleichungen lösen kann, findest du im Kapitel Bruchgleichungen.)
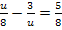
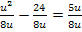
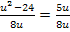 |
| 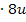
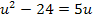
Jetzt erkennt man, dass eine gemischtquadratische Gleichung vorliegt, da 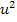 und u vorkommen. Bevor wir die Mitternachtsformel anwenden können, muss die Gleichung noch nach Null aufgelöst werden.
und u vorkommen. Bevor wir die Mitternachtsformel anwenden können, muss die Gleichung noch nach Null aufgelöst werden.
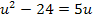
![]() |
| 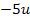
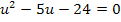
Mit der Mitternachtsformel erhalten wir:
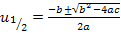
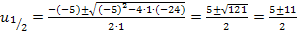
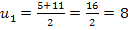
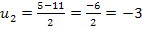
Jetzt kommt wieder die Rücksubstitution.
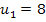 in
in 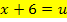

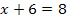 |
| 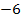
![]()
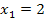
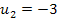 in
in 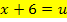

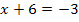 |
| 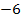
![]()
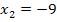
Wir überprüfen noch, ob die beiden soeben berechneten Werte 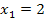 und
und 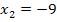 in der Definitionsmenge enthalten sind. Da x alle reellen Zahlen außer -6 annehmen darf, liegen beide Werte innerhalb der Definitionsmenge und sind somit wirklich Lösungen der Gleichung. Fertig!
in der Definitionsmenge enthalten sind. Da x alle reellen Zahlen außer -6 annehmen darf, liegen beide Werte innerhalb der Definitionsmenge und sind somit wirklich Lösungen der Gleichung. Fertig!
zu c.)
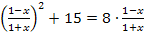
Puh, das ist aber eine Monsteraufgabe! Naja, gehen wir wie schon bei den anderen Aufgaben a.) und b.) vor. Es handelt sich wie schon bei b.) um eine Bruchgleichung, da x im Nenner vorkommt. Also bestimmen wir zuerst die Definitionsmenge D. du erkennst ohne weitere Rechnung, dass x nicht -1 sein darf, da sonst der Nenner Null wird. Alle anderen reellen Zahlen kann man einsetzen für x. Es gilt daher:
D = ℝ 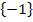
So weit, so gut. Aber wie löst man denn dieses Ding nach x auf? Hier hilft uns wieder eine Substitution. Wenn du die Gleichung genau betrachtest, findest du vielleicht selbst heraus, was wir hier durch u ersetzen. Tipp:Suche nach einem Ausdruck, der mehrmals in gleicher Form auftaucht!

