Substitution

Das Problem besteht allerdings darin, dies überhaupt zu erkennen und eben eine „geeignete“ Substitution durchzuführen. Bloßwas ist denn geeignet? Das kann man nicht allgemein sagen. Welchen mathematischen Ausdruck man gleich u setzt, hängt nämlich ganz von der vorliegenden Gleichung ab. Man muss im Prinzip oft so substituieren, dass letztendlich eine Gleichung der Form 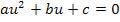entsteht. Wie das geht, kannst du im nächsten Beispiel sehen.

10. Bsp.:

(Nicht Stoff der Realschule, aber extrem wichtig für Gymnasiasten der 9. Klasse)

Führe zuerst eine geeignete Substitution durch und löse dann die folgenden Gleichungen!

a.)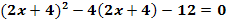

b.)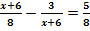

c.)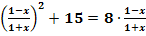

Lösung:

zu a.)

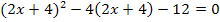
Wir sollen eine Substitution machen, d.h. eine neue Variable einführen, damit eine einfacher zu lösende Gleichung entsteht. Hier erkennt man eigentlich recht gut, welchen Ausdruck man durch die neue Variable, z.B. u, ersetzt. Du findest es bestimmt selbst heraus! Wenn doch nicht, schau´dir einfach die nächste Zeile an!

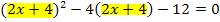
Jetzt hast du sicher erkannt, dass der Ausdruck 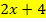 einmal zum Quadrat und einmal ohne Quadrat vorkommt, und sich daher die folgende Substitution anbietet:

Subst.: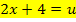

Wir führen also die neue Variable u ein, um die Gleichung zu vereinfachen. Schreiben wir in der Gleichung an Stelle von 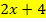einfach u, erhalten wir die folgende gemischtquadratische Gleichung mit der neuen Variablen u:

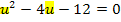
Wir lösen sie mit der Mitternachtsformel nach u auf.

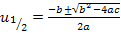
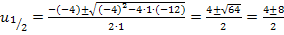
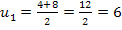
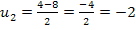
Nun wissen wir zwar, was u ist, aber noch nicht, was x ist, und genau das müssen wir schließlich ermitteln. Dazu führen wir die sogenannte Rücksubstitution durch:In die oben gelb unterlegte Gleichung 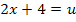setzen wir für u die soeben ermittelten Werte ein:D.h. einmal wird der Wert 6 und einmal den andere Wert -2 für u eingesetzt. So erhalten wir zwei Gleichungen, die nun wieder x als Unbekannte enthalten. sie lassen sich leicht jeweils nach x auflösen.

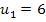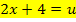
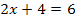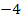
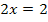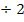
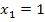
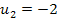in |

|

in |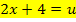

|

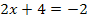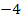
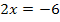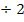
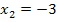
So, jetzt sind wir fertig! Manch ein Schüler mag sich nun denken, dass man diese Gleichung doch auch ohne Substitution hätte lösen können. Das stimmt natürlich. Die erste Klammer hätte man auch mit der ersten binomischen Formel ausrechnen können. Die zweite Klammer hätte sich leicht ausmultiplizieren lassen. Nachdem man dann alles soweit möglich zusammengefasst hätte, ließe sich ebenfalls die Mitternachtsformel anwenden und somit die Gleichung nach x auflösen. In diesem Fall hätte das normale Ausrechnen auch relativ schnell zur Lösung geführt. Doch wird in den nächsten beiden Beispielen, vor allem im Bsp. c.) klar, dass eine geeignete Substitution wirklich eine Erleichterung darstellt.

---