Stochastisch unabhängige Ereignisse (Produktsatz)
P(A) = 2% = 0,02
Die Wahrscheinlichkeit für mindestens einen Fehler beträgt 6,9%. Wenn mindestens ein Fehler eintritt, bedeutet das, dass entweder genau ein Fehler oder beide zugleich eintreten. Das entspricht dem Ereignis A oder auch B, also A 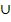 B. P(A
B. P(A 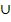 B) = 6,9% = 0,069
B) = 6,9% = 0,069
Erinnere dich an die Formel für Oder-Ereignisse, den sogenannten Satz von Sylvester (auch Additionssatz genannt):
P(A 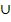 B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A 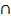 B)
B)
0,069 = 0,02 + P(B) – P(A 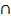 B)
B)![]() (Gleichung I)
(Gleichung I)
Da die beiden Fehler A und B unabhängig auftreten, gilt:
P(A 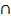 B) = P(A)
B) = P(A)  P(B)
P(B)
P(A 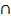 B) = 0,02
B) = 0,02  P(B)
P(B)![]() (Gleichung II)
(Gleichung II)
Man kann nun die Gleichung II in die Gleichung I einsetzen. So erhält man eine Gleichung, die als einzige Unbekannte P(B) enthält. Damit kann die in Teilaufgabe a) gesuchte Wahrscheinlichkeit P(B) berechnet werden.
II in I: 0,069 = 0,02 + P(B) – 0,02  P(B)
P(B)![]() | – 0,02
| – 0,02
![]() 0,049 = 0,98
0,049 = 0,98  P(B)
P(B)![]() |
| 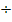 0,98
0,98
![]() P(B) = 0,05 = 5%
P(B) = 0,05 = 5%
In Teilaufgabe b) ist nach der Wahrscheinlichkeit gefragt, dass keiner der beiden Fehler auftritt. Gesucht ist also P( 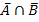 ). Man kann diese Wahrscheinlichkeit auf verschiedene Weise berechnen. Der umständlichste Weg wäre es, P(
). Man kann diese Wahrscheinlichkeit auf verschiedene Weise berechnen. Der umständlichste Weg wäre es, P( 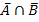 ) mit einer Vierfeldertafel zu ermitteln. Darauf soll hier verzichtet werden. Da die beiden Ereignisse A und B stochastisch unabhängig sind, bietet sich folgender Weg an:
) mit einer Vierfeldertafel zu ermitteln. Darauf soll hier verzichtet werden. Da die beiden Ereignisse A und B stochastisch unabhängig sind, bietet sich folgender Weg an:
P( 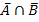 ) = P(
) = P( 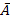 )
)  P(
P( 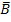 )
)
Geg.:P(A) = 0,02 P(B) = 0,05
Die Wahrscheinlichkeiten der Gegenereignisse lassen sich bekanntlich berechnen, indem man die Wahrscheinlichkeit des jeweiligen Ereignisses von 1 subtrahiert. So erhält man:
P( 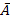 ) = 1- P(A) = 1 – 0,02 = 0,98
) = 1- P(A) = 1 – 0,02 = 0,98
P( 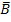 ) = 1 – P(B) = 1- 0,05 = 0,95
) = 1 – P(B) = 1- 0,05 = 0,95
P( 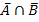 ) = P(
) = P( 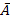 )
)  P(
P( 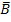 ) = 0,98
) = 0,98  0,95 = 0,931 = 93,1%
0,95 = 0,931 = 93,1%
Eine weitere, sehr geschickte Methode zur Berechnung von P( 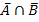 ) ist die Verwendung des Gegenereignisses von
) ist die Verwendung des Gegenereignisses von 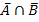 . Das Gegenereignis zu „kein Fehler“ ist logischerweise „mindestens ein Fehler“. Die Wahrscheinlichkeit für „mindestens ein Fehler“ P(A
. Das Gegenereignis zu „kein Fehler“ ist logischerweise „mindestens ein Fehler“. Die Wahrscheinlichkeit für „mindestens ein Fehler“ P(A 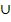 B) ist laut Angabe P(A
B) ist laut Angabe P(A 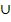 B) = 6,9% = 0,069. Man braucht diesen Wert nur von 100% bzw. 1 abziehen und erhält sofort die gesuchte Wahrscheinlichkeit P(
B) = 6,9% = 0,069. Man braucht diesen Wert nur von 100% bzw. 1 abziehen und erhält sofort die gesuchte Wahrscheinlichkeit P( 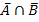 ).
).
P( 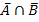 ) = 1 – 0,069 = 0,931 = 93,1%
) = 1 – 0,069 = 0,931 = 93,1%
Wir erhalten auf diesem Weg natürlich das gleiche Ergebnis wie oben.

