Stochastisch unabhängige Ereignisse (Produktsatz)
Wir müssen nur noch überprüfen, ob die Gleichung P(W 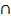 S) = P(W)
S) = P(W)  P(S) erfüllt ist.
P(S) erfüllt ist.
P(W)  P(S) = 0,8
P(S) = 0,8  0,6 = 0,48
0,6 = 0,48 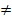 0,55
0,55
P(W 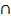 S)
S) 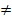 P(W)
P(W)  P(S)
P(S)  W und S stochastisch abhängig
W und S stochastisch abhängig
Die Aufgabe ist damit gelöst. Zur Vertiefung des Begriffs der stochastischen Abhängigkeit solltest du dir zusätzlich folgende Tatsachen bewusst machen:
Der Anteil der weiblichen Mitglieder unter den Schülern ist nicht gleich dem Anteil der weiblichen Mitglieder bei den Nicht-Schülern. Es hängt davon ab, innerhalb welcher Gruppe man den Anteil der Frauen bestimmen soll.
Auch der Anteil der Schüler unter den Frauen unterscheidet sich vom Anteil der Schüler unter den Männern. Es hängt davon ab, innerhalb welcher Gruppe man den Anteil der Schüler ermitteln soll.
4. Bsp.:
Bei der Produktion von Fußbällen treten zwei verschiedene, stochastisch unabhängige Fehler A und B auf. Fehler A tritt mit einer Wahrscheinlichkeit von 2% auf. Mindestens einer der beiden Fehler findet sich in 6,9% aller Fälle.
a) Mit welcher Wahrscheinlichkeit tritt der Fehler B auf?
b) Mit welcher Wahrscheinlichkeit tritt gar kein Fehler auf?
c) Mit welcher Wahrscheinlichkeit tritt genau einer der Fehler auf?
d) Mit welcher Wahrscheinlichkeit tritt höchstens ein Fehler auf?
Lösung:
Laut Angabe ist die Wahrscheinlichkeit für den Fehler A gleich 2%.

