Stochastisch unabhängige Ereignisse (Produktsatz)

Nun können wir ganz leicht die Formel der Unabhängigkeit herleiten. Dazu verwenden wir den obersten Ast des Baumdiagramms. Nach der 1. Pfadregel gilt:

I.         P(B 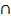I) = P(B)

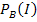
Da B und I unabhängige Ereignisse sind (die Intelligenz hängt schließlich nicht von der Haarfarbe ab, auch wenn oft Gegenteiliges behauptet wird), gilt außerdem:

II. 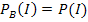       (Das haben wir oben schließlich gezeigt.)

Setzt man Gleichung II. in I. ein, ergibt sich schon die gewünschte Formel:

P(B 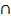I) = P(B) P(I)

Da nur bei unabhängigen Ereignissen die beiden bedingten Wahrscheinlichkeiten 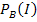und 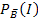sowie die totale Wahrscheinlichkeit P(I) gleich großsind, gilt die gerade hergeleitete Formel P(B 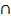I) = P(B) P(I) nur bei unabhängigen Ereignissen.

P(B 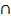I) = P(B) P(I) ⇔        B und I sind (stochastisch) unabhängig.

Nun folgen einige typische Aufgabenbeispiele zur stochastischen Unabhängigkeit.

3. Bsp.:

Der Reitverein Hoppereit hat 240 Mitglieder. 192 der Mitglieder sind weiblich (W). 144 der Reitvereinsmitglieder gehen noch zur Schule (S). 36 Mitglieder sind männlich und gehen nicht mehr zur Schule. Überprüfe die Ereignisse W und S auf stochastische Unabhängigkeit! Verwende dazu eine vollständig ausgefüllte Vierfeldertafel!

Lösung:

Die Ereignisse W und S wären stochastisch unabhängig, wenn gilt:

P(W 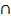S) = P(W) P(S)

Das gilt es nun zu überprüfen.

---