Stochastisch unabhängige Ereignisse (Produktsatz)

1. Bsp.:

Im Land Absurdinien gibt es insgesamt 40% Männer (M). 5% der Männer in diesem Land haben eine Blutgerinnungsstörung. Bei den Frauen dieses Landes tritt diese Blutgerinnungsstörung nur mit einer Wahrscheinlichkeit von 1% auf. Personen, die an dieser Blutgerinnungsstörung leiden, werden im Folgenden unabhängig von ihrem Geschlecht als Bluter (B) bezeichnet.

Zeigen Sie, dass die Ereignisse Mann M und Bluter B stochastisch abhängig sind!

Lösung:

Wir schreiben uns erst einmal jede Angabe aus dem Text mit der mathematisch korrekten Schreibweise für die entsprechende Wahrscheinlichkeit heraus:

Geg.:

Wahrscheinlichkeit für „Mann“ (insgesamt): P(M) = 40% = 0,4

Wahrscheinlichkeit für Bluter, wenn Mann: 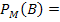5% = 0,05

Wahrscheinlichkeit für Bluter, wenn Frau/Nicht-Mann: 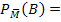     1% = 0,01

Offensichtlich unterscheidet sich der Anteil der Bluter unter den Männern 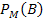vom Anteil der Bluter unter den Frauen 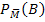. Es hängt also davon ab, ob man innerhalb der Gruppe der Männer oder in der Gruppe der Frauen nach Blutern sucht. Die beiden bedingten Wahrscheinlichkeiten 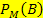und 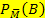sind unterschiedlich hoch;daran erkennt man sofort, dass die beiden Ereignisse M und B abhängig sind.

Das wollen wir nun rechnerisch nachweisen.

Für unabhängige Ereignisse gilt:

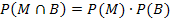
Da die Ereignisse M und B jedoch abhängig sind, müssen wir zeigen, dass diese Formel nicht gilt. Dafür benötigen wir noch die Wahrscheinlichkeiten 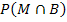und 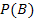. Wir ermitteln sie mit Hilfe des folgenden Baumdiagramms. Siehe unten!

Die UND-Wahrscheinlichkeit 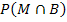wird mit der 1. Pfadregel durch Multiplikation der Wahrscheinlichkeiten entlang des obersten Pfades berechnet.

---