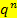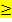Stochastisch unabhängige Ereignisse (Produktsatz)

Es wird also durch eine negative Zahl geteilt. Daher dreht sich das Ungleichheitszeichen an dieser Stelle noch einmal um! Der Logarithmus einer Zahl unter 1 ist immer negativ. Da sich der Logarithmus bei diesem Aufgabentyp immer auf die Nietenwahrscheinlichkeit bezieht und diese Wahrscheinlichkeit immer kleiner als 1 ist, muss du bei der Division durch den Logarithmus bei diesen Aufgaben immer das Ungleichheitszeichen umdrehen!)

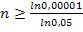
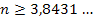
Da es sich bei n um die Anzahl der Dieselgeneratoren handelt, muss n eine ganze Zahl sein. Wir runden wegen des Größer-Gleichzeichens auf. Achtung:Es wird nicht wegen der Ziffer 8 hinter dem Komma aufgerundet! Bei Größer- oder Größer-Gleichzeichen muss immer aufgerundet werden, egal was hinter dem Komma steht! Man sucht ja die nächst größere ganze Zahl, die die Ungleichung erfüllt, und nicht eine kleinere.

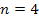
Es müssen also mindestens vier Dieselgeneratoren bereitgestellt werden, damit mit mindestens 99,999% Wahrscheinlichkeit mindestens einer arbeitet, wenn es zum Ausfall der externen Stromversorgung kommt.

Wenn ihr eine Aufgabe dieses Typs im Schulunterricht besprochen habt, wird eine ähnliche Aufgabe mit größter Wahrscheinlichkeit in der nächsten Schulaufgabe oder Extemporale gestellt werden. Übe diese Art von Aufgaben so oft wie möglich! Zur Erleichterung soll dir folgende allgemeine Anleitung dienen:

Aufgabenstellung der „Dreimal-Mindestens-Aufgaben“ allgemein: Wie oft muss ein Versuch mindestens ausgeführt werden, damit mit mindestens … % Wahrscheinlichkeit mindestens ein Treffer (konstante Trefferwahrscheinlichkeit p) auftritt? Ges.: Anzahl der Versuche n X steht für die Anzahl der Treffer Geg.: Trefferwahrscheinlichkeit p      Nietenwahrscheinlichkeit q = 1 – p P(X 1) … % 1 – P(X = 0) … % 1- … %

Hinweis:Die Trefferwahrscheinlichkeit p (klein geschrieben) bezieht sich immer auf einen einzelnen Versuch. Die Wahrscheinlichkeit P (großgeschrieben) bezieht sich dagegen immer auf alle n Versuche insgesamt. Nur wenn alle Versuche unabhängig voneinander sind, bleibt p konstant. Der oben gezeigte Lösungsansatz darf nur dann verwendet werden.

Manchmal wird auch nach der Mindestanzahl der Versuche gefragt, so dass sich mit mehr als … % Wahrscheinlichkeit mindestens ein Treffer ergibt. Dann fällt das Gleichzeichen unter dem Größer-Gleichzeichen weg. Du verwendest dann den Ansatz:   P(X 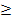1) … %

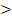Die „Dreimal-Mindestens-Aufgaben“ werden auch im Zusammenhang mit der Binomial-Verteilung bzw. der Bernoulli-Kette behandelt. Näheres dazu findest du im Kapitel Bernoulli-Kette und Binomial-Verteilung.

---