Stochastisch unabhängige Ereignisse (Produktsatz)

Die Ausfallwahrscheinlichkeit eines einzelnen Dieselgenerators beträgt 5% = 0,05.

Wir nennen die gesuchte Anzahl der Dieselgeneratoren n. Es handelt sich bei dieser Aufgabe um eine sogenannte „Dreimal-Mindestens-Aufgabe“, da im Text dreimal das Wort „mindestens“ vorkommt. Solche Aufgaben werden sehr oft gestellt. (Manchmal wird in solchen Aufgaben statt dem Wort „mindestens“ auch das gleichbedeutende „wenigstens“ verwendet. Außerdem gibt es auch ähnliche Aufgaben, in denen nach der Mindestanzahl n der Versuche gefragt wird, die benötigt werden, damit mit einer Wahrscheinlichkeit von mehr als …% mindestens ein Treffer erzielt wird. Dabei muss dann statt 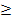das Zeichen 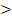in der Rechnung verwendet werden. Am Prinzip der Rechnung ändert sich jedoch nichts.)

Die Wahrscheinlichkeit, dass mindestens ein Generator arbeitet, lässt sich am leichtesten mit Hilfe des Gegenereignisses berechnen. Das Gegenereignis zu „ mindestens einer arbeitet“ lautet „keiner arbeitet“ bzw. „alle n Generatoren fallen aus“.

Wir bezeichnen die Anzahl der Generatoren, die arbeiten, mit X. Somit gelten folgende mathematische Abkürzungen:

P(mindestens ein Generator arbeitet) = P(X 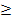1)

P(Kein Generator arbeitet) = P(X = 0)

Die Wahrscheinlichkeit, dass mindestens ein Generator arbeitet, soll mindestens 99,999% betragen.

P(X 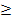1) 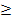99,999%

P(X 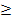1) 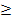0,99999

Da das Ereignis „kein Generator arbeitet“ das Gegenereignis zu „mindestens ein Generator arbeitet“ ist, gilt:

1 – P(X = 0) 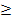0,99999

Die Wahrscheinlichkeit P(X = 0), dafür dass kein Generator arbeitet bzw. dass alle n Generatoren ausfallen, lässt sich berechnen durch 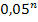. (Vergleiche dazu den in Teilaufgabe a) gezeigten Baum! Dieses Baumdiagramm stellt die Situation am Beispiel n = 3 dar.)

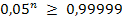
1 – | – 1

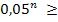- – 0,0000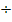1 | (-1) Achtung:Ungleichheitszeichen umdrehen wegen der Division durch eine negative Zahl! (Zur Erinnerung:Bei Multiplikation oder Division durch eine negative Zahl dreht sich in einer Ungleichung das Ungleichheitszeichen um.)

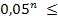0,00001 |ln        (Es könnte z.B. auch der Zehnerlogarithmus lg verwendet werden, um nach n aufzulösen. Der Logarithmus muss immer dann angewendet werden, wenn der Exponent, also die Hochzahl gesucht ist.)

ln( 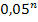) 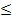ln0,00001

Nun wird das Logarithmus-Rechengesetz 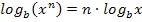 bzw. 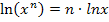 angewendet:

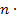ln0,05 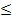ln0,00001 | 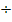ln0,05         (Vorsicht:ln0,05 ist negativ!

---