Stochastisch unabhängige Ereignisse (Produktsatz)
Lösung:
a) Laut Angabe arbeiten die Dieselgeneratoren unabhängig voneinander. Jeder einzelne fällt mit einer Wahrscheinlichkeit von 5% aus. Gefragt ist in dieser Teilaufgabe nach der Wahrscheinlichkeit, dass keiner der drei Dieselgeneratoren arbeitet, dass also alle drei Dieselgeneratoren gleichzeitig ausfallen. Es sollen also der erste, der zweite und der dritte Generator ausfallen. Da die einzelnen Generatoren unabhängig arbeiten, fallen sie auch unabhängig voneinander aus. Die einzelnen Ausfallwahrscheinlichkeiten dürfen deshalb einfach miteinander multipliziert werden.
P(Keiner der 3 Generatoren arbeitet) = P(Alle 3 Generatoren fallen aus) = 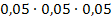 =
= 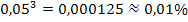
Man kann dies auch an einem Baumdiagramm erkennen. Allerdings brauchen wir eigentlich nur den obersten Ast des unten dargestellten Baumdiagramms. Daher musst du natürlich nicht das ganze Baumdiagramm zeichnen, um diese Aufgabe zu lösen. Hier ist es nur der Übersicht wegen komplett gezeigt.
F steht für „Dieselgenerator fällt aus“
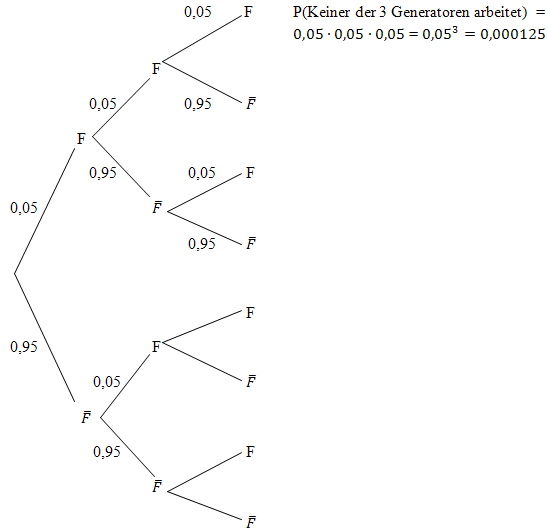
In Teilaufgabe b) ist nach der Anzahl der Dieselgeneratoren gefragt, die man mindestens benötigt, damit mit mindestens 99,999% Wahrscheinlichkeit mindestens einer arbeitet.

