Stochastisch unabhängige Ereignisse (Produktsatz)
In Teilaufgabe c) ist nach der Wahrscheinlichkeit für genau einen Fehler gefragt. In anderen Worten nach der Wahrscheinlichkeit, dass nur Fehler A oder nur Fehler B eintritt, also dass A eintritt, aber B nicht oder A nicht eintritt, jedoch aber B.
Geg.: P(A) = 0,02 P(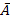 
) = 0,98 P(B) = 0,05 P( 
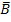) = 0,95
Ges.: P(A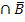 
) + P( 
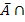B)
Da die beiden Ereignisse A und B unabhängig sind, gilt:
P(A 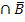) + P( 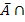B) = P(A) 
P( ) + P( 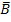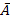) P(B)
P(A 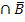) + P( 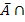B) = 0,02 0,95 + 0,98 0,05 = 0,068 = 6,8%
In Teilaufgabe d) ist nach der Wahrscheinlichkeit für höchstens einen Fehler gefragt. In anderen Worten nach der Wahrscheinlichkeit, dass entweder keiner der beiden Fehler eintritt oder genau einer. Man kann also die beiden in den Teilaufgaben b) und c) ermittelten Wahrscheinlichkeiten einfach addieren, um die nun gesuchte Wahrscheinlichkeit zu erhalten.
P(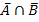 
) +[ P(A 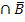) + P( 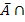B)] = 0,931+ 0,068 = 0,999 = 99,9%
Eine andere elegante Methode, die Wahrscheinlichkeit für höchstens einen der beiden Fehler zu berechnen, verwendet das Gegenereignis. Das Gegenereignis zu „höchstens ein Fehler von Zweien“ lautet „beide Fehler (zugleich)“. Die Wahrscheinlichkeit dafür, dass beide Fehler eintreten, lässt sich schnell berechnen, da die beiden Ereignisse A und B unabhängig sind.
P(A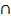 
B) = P(A) P(B) = 0,02 0,05 = 0,001
P(höchstens ein Fehler) = P(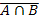 
) = 1- P(A 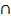B) = 1 – 0,001 = 0,999 = 99,9%
Wie erwartet, erhalten wir das gleiche Ergebnis. Mit Hilfe einer Vierfeldertafel wäre man auch zu diesem Ergebnis gekommen, man hätte nur die Wahrscheinlichkeiten P( 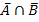), P(A 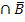) und P( 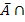B) addieren müssen. Du solltest alle drei erwähnten Rechenwege nachvollziehen können;die Entscheidung, welchen Weg du letztendlich selbst verwendest, bleibt dir überlassen. Das ist einfach Geschmacksache. Das gilt auch für die in Teilaufgabe b) und c) gezeigten Varianten.
Im Folgenden findest du ein Aufgabenbeispiel etwas anderer Art, das aber auch extrem wichtig ist. Es leitet über zu den sogenannten „Dreimal-Mindestens-Aufgaben“, die ab der 10.Klasse des Gymnasiums (FOS / BOS 11. oder 12.Klasse) einen sehr häufig gestellten Aufgabentyp darstellen. Auch in der Abiturprüfung ist mit einer Aufgabe dieses Typs zu rechnen.
Bisher wurden immer zwei Ereignisse auf Unabhängigkeit überprüft oder es waren zwei unabhängige Ereignisse gegeben. Nun wird ein Zufallsexperiment immer wieder in gleicher Weise wiederholt. Die einzelnen Versuche sollen dabei unabhängig voneinander sein, d.h. sie sollen sich gegenseitig nicht beeinflussen.
