Stochastisch unabhängige Ereignisse (Produktsatz)
In diesem Kapitel wird die Kenntnis des Begriffs der bedingten Wahrscheinlichkeit vorausgesetzt. Sollte dir die Schreibweise 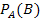 nichts sagen, befasse dich zuerst mit dem Thema Bedingte Wahrscheinlichkeit!
nichts sagen, befasse dich zuerst mit dem Thema Bedingte Wahrscheinlichkeit!
| Definition:
Zwei Ereignisse A und B sind genau dann stochastisch unabhängig, wenn gilt:
Das ist immer dann der Fall, wenn gilt:
Andernfalls heißen sie stochastisch abhängig. |
Die Formel 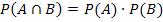 für stochastisch unabhängige Ereignisse ist leicht zu merken mit dem folgenden Satz:Und ist gleich Mal, wenn unabhängig.
für stochastisch unabhängige Ereignisse ist leicht zu merken mit dem folgenden Satz:Und ist gleich Mal, wenn unabhängig.
Du findest diese Formel aber auch in deiner Formelsammlung im Stochastik-Teil unter dem Stichwort „Unabhängigkeit“.
Vorsicht:In der analytischen Geometrie gibt es den Begriff der linearen Unabhängigkeit bzw. Abhängigkeit von Vektoren. Das ist natürlich etwas ganz anderes als die stochastische Unabhängigkeit bzw. Abhängigkeit zweier Ereignisse! Mehr über linear abhängige bzw. unabhängige Vektoren findest du im Bereich analytische Geometrie im Kapitel Lineare Abhängigkeit.
Im Folgenden werden auf dieser web-site statt den ziemlich langen Begriffen „stochastisch unabhängig“ und „stochastisch abhängig“ einfach die Bezeichnungen „unabhängig“ bzw. „abhängig“ verwendet. Da wir uns momentan nur mit Stochastik und nicht mit analytischer Geometrie befassen, besteht schließlich keine Verwechslungsgefahr.
Wie oben in der Definition schon erwähnt, gilt für zwei unabhängige Ereignisse A und B:
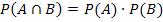
Mit dieser Formel zu rechnen, ist natürlich ganz einfach;was es aber anschaulich bedeutet, dass zwei Ereignisse stochastisch unabhängig sind, erschließt sich nicht sofort. Um den Begriff der Abhängigkeit bzw. Unabhängigkeit zweier Ereignisse zu erklären, wird zuerst ein Beispiel abhängiger Ereignisse vorgeführt.

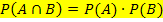 (Produktsatz)
(Produktsatz)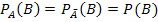 und
und