Bedingte Wahrscheinlichkeit
In Teilaufgabe d) ist ebenfalls nach einer bedingten Wahrscheinlichkeit gefragt, nämlich nach der Wahrscheinlichkeit, dass ein Pferd, das nicht mit dem Virus infiziert ist, trotzdem hustet. Es handelt sich also um ein Pferd, das nicht mit dem Virus infiziert ist. Bedingung ist daher Nicht-Virus infiziert  (Bedingung
(Bedingung  als Index tiefer gesetzt). Die Frage war ja, mit welcher Wahrscheinlichkeit es trotzdem hustet? Gesucht ist daher die Wahrscheinlichkeit
als Index tiefer gesetzt). Die Frage war ja, mit welcher Wahrscheinlichkeit es trotzdem hustet? Gesucht ist daher die Wahrscheinlichkeit  . Sie steht im Baumdiagramm Nr.2 am dritten Pfad von oben an der hinteren Verzweigung.
. Sie steht im Baumdiagramm Nr.2 am dritten Pfad von oben an der hinteren Verzweigung.
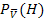 kann entweder am Baum Nr.2 mit Hilfe der 1.Pfadregel und Umstellen oder direkt mit der Formel für die bedingte Wahrscheinlichkeit
kann entweder am Baum Nr.2 mit Hilfe der 1.Pfadregel und Umstellen oder direkt mit der Formel für die bedingte Wahrscheinlichkeit 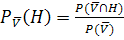
berechnet werden.
Die Wahrscheinlichkeit P(  ) berechnet man mit P(
) berechnet man mit P(  ) = 1 –
) = 1 – 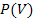 = 1- 0,12 = 0,88
= 1- 0,12 = 0,88
Außerdem benötigt man noch die Wahrscheinlichkeit 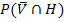 . Da es beim Schnitt zweier Mengen nicht auf die Reihenfolge ankommt, gilt:
. Da es beim Schnitt zweier Mengen nicht auf die Reihenfolge ankommt, gilt:
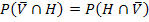
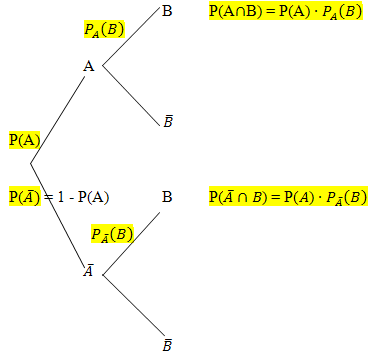
Man kann 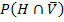 ganz leicht am Baum Nr.1 (Zweiter Ast von oben) mit der 1. Pfadregel berechnen:Einfach die Wahrscheinlichkeiten entlang des Pfades multiplizieren!
ganz leicht am Baum Nr.1 (Zweiter Ast von oben) mit der 1. Pfadregel berechnen:Einfach die Wahrscheinlichkeiten entlang des Pfades multiplizieren!
P( 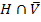 ) = P(H)
) = P(H) 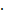
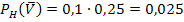
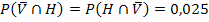
Die Wahrscheinlichkeiten P( 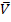 ) = 0,88 und
) = 0,88 und 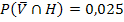 können in das Baumdiagramm Nr.2 eingetragen werden.
können in das Baumdiagramm Nr.2 eingetragen werden.
P( 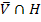 ) = P(
) = P( 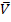 )
) 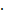
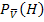
![]()

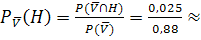 0,0284 = 2,84%
0,0284 = 2,84%
2,84% der Pferde, die nicht von dem Virus befallen sind, haben trotzdem Husten.
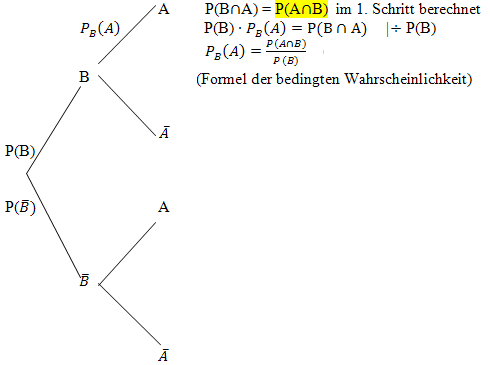
Anleitung zur Berechnung der bedingten Wahrscheinlichkeit 
Geg.: Ges.: Baum Nr.1 1. Schritt:Wahrscheinlichkeiten am obersten Ast multiplizieren
2. Schritt: Wahrscheinlichkeiten am dritten Ast von oben multiplizieren
3. Schritt:Diese beiden Wahrscheinlichkeiten addieren
4. Schritt:Bedingte Wahrscheinlichkeit mit der Formel oder mit Hilfe des umgekehrten Baums berechnen
Alternativ dazu die Berechnung von
Baum Nr.2 Zur Berechnung einer anderen bedingten Wahrscheinlichkeit, verwendest du natürlich einen anderen Ast, nämlich denjenigen, an dem die entsprechende bedingte Wahrscheinlichkeit im Baum Nr.2 steht. Dazu brauchst du die entsprechende UND-Wahrscheinlichkeit. Du berechnest sie am 1. Baum. Vorsicht:Sie kann auf einer anderen Höhe stehen! |
Anspruchsvolle Aufgabenbeispiele:
Jetzt wird es wirklich schwierig! Bearbeite das 3. Bsp. nur, wenn du eine besondere Herausforderung suchst oder zur Abiturvorbereitung! Schüler der 10. Klasse des G8 können auch gleich mit dem 4. Bsp. fortfahren.

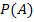
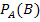
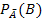
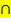 B) = P(A)
B) = P(A) 
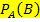
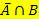 ) = P(
) = P( 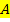 )
) 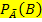
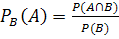 (Formel für die bedingte Wahrscheinlichkeit)
(Formel für die bedingte Wahrscheinlichkeit)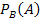 mit dem umgekehrten Baumdiagramm:
mit dem umgekehrten Baumdiagramm: A) = P(A
A) = P(A