Bedingte Wahrscheinlichkeit
In Teilaufgabe a) soll ermittelt werden, wie hoch die Wahrscheinlichkeit ist, dass ein Pferd hustet und den Virus in sich trägt, also P(H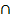 
V). Vorsicht:Hier ist eine UND-Wahrscheinlichkeit gesucht und keine bedingte Wahrscheinlichkeit! Die gesuchte UND-Wahrscheinlichkeit P(H 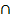V) steht im unten dargestellten Baumdiagramm Nr.1 hinter dem obersten Ast. Sie kann leicht mit Hilfe der 1. Pfadregel berechnet werden:Einfach die Wahrscheinlichkeiten entlang des obersten Pfades multiplizieren! Vergleiche Baumdiagramm Nr.1!
P(H 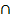V) = P(H)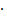 
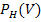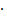= 0,1 0,75 = 0,075 = 7,5%
7,5% aller Pferde haben Husten und sind gleichzeitig mit dem Virus infiziert.
In Teilaufgabe b) soll ermittelt werden, wie hoch die Wahrscheinlichkeit ist, dass ein Pferd mit dem Virus infiziert ist, also die totale Wahrscheinlichkeit P(V). Man kann P(V) entweder mit einer Vierfeldertafel berechnen oder einfach durch Addition von P(H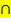 
V) und P( 
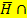V), da die hustenden, virusinfizierten Pferde H 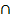V und die nicht-hustenden, virusinfizierten Pferde 
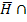V zusammen alle virusinfizierten Pferde V ergeben. Die Wahrscheinlichkeit P( 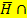V) wird wieder nach der 1. Pfadregel durch Multiplikation der Wahrscheinlichkeiten entlang des entsprechenden Pfades berechnet:P( 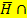V) = P( 
) 
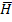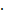
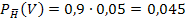
P(V) = P(H 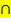V) + P( 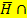V) = 0,075 + 0,045 = 0,12 = 12%
12% aller Pferde sind also von dem Virus befallen.
P(V) kann im Baumdiagramm Nr.1 jedoch nicht eingetragen werden, dazu brauchen wir das umgekehrte Baumdiagramm Nr.2. Siehe unten!
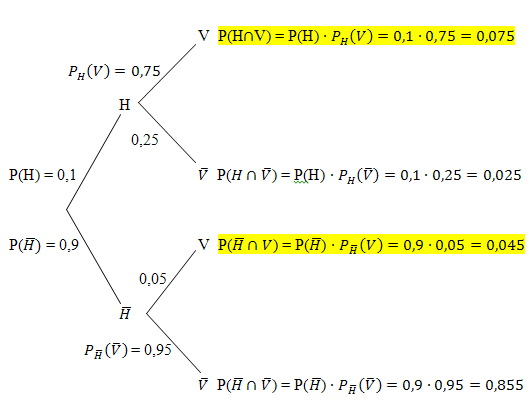
Baumdiagramm Nr.1
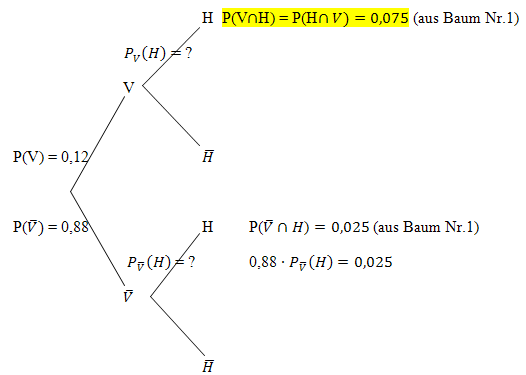
Baumdiagramm Nr.2
In Teilaufgabe c) ist nach der (bedingten) Wahrscheinlichkeit gefragt, dass ein Pferd, das von dem Virus befallen ist, hustet. In anderen Worten:Wenn ein Pferd von dem Virus befallen ist, mit welcher Wahrscheinlichkeit hustet es dann? Oder noch mal anders formuliert:Es ist ein Pferd, das mit dem Virus infiziert ist;mit welcher Wahrscheinlichkeit hustet es dann? Die Bedingung ist daher V (Virus infiziert). Gesucht ist also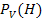 
. Diese Wahrscheinlichkeit steht im Baumdiagramm Nr.2 an der hinteren Verzweigung am obersten Ast. Da in den Teilaufgaben a) und b) die Wahrscheinlichkeiten P(V) = 0,12 und P(V 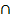H) = P(H 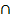V) = 0,075 schon berechnet wurden, ist es kein Problem die gesuchte Wahrscheinlichkeit 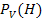entweder mit der 1. Pfadregel am Baum Nr.2 und Umformen nach 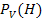oder direkt mit der Formel für die bedingte Wahrscheinlichkeit 
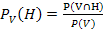zu berechnen:
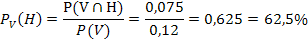
Es haben daher 62,5% der virus-infizierten Pferde Husten.
