Bedingte Wahrscheinlichkeit
2. Bsp.:
Pferde können durch ein besonderes Virus befallen werden, welches zu schwerem Husten und Lungenentzündung führen kann. Nicht jedes Pferd, das hustet, muss aber die erwähnte Virusinfektion haben und nicht alle hustenden Pferde sind von dem Virus befallen. 10% aller Pferde haben Husten. Aus Erfahrung weißman, dass von diesen Pferden 75% mit dem oben beschriebenen Virus infiziert sind. Aber auch 5% der Pferde, die nicht husten und gesund zu sein scheinen, sind in Wirklichkeit von dem Virus befallen.
Wie hoch ist die Wahrscheinlichkeit, dass …
a) ein Pferd hustet und den Virus in sich trägt?
b) ein Pferd mit dem Virus infiziert ist?
c) ein Pferd, das von dem Virus befallen ist, hustet?
d) ein Pferd, das nicht mit dem Virus infiziert ist, trotzdem hustet?
Lösung:
Wir verwenden folgende Abkürzungen:
V für „Pferd ist tatsächlich von dem Virus befallen“
H für „Pferd hat Husten“
Nun überlegen wir uns, wie die Angaben im Text als Wahrscheinlichkeiten mathematisch korrekt geschrieben werden können.
Aus dem Text:
10% aller Pferde haben Husten 
P(H) = 10% = 0,1
Es handelt sich dabei um eine totale Wahrscheinlichkeit, da sie sich auf alle Pferde, also die Gesamtheit bezieht.
Von diesen Pferden (also den hustenden Pferden) sind 75% mit dem oben beschriebenen Virus infiziert.
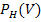= 75% = 0,75
Es handelt sich hierbei um eine bedingte Wahrscheinlichkeit, da sie sich nur auf die hustenden Pferde bezieht. Husten H ist daher die Bedingung (als Index tiefergestellt). Man hätte das auch anders sagen können:Wenn ein Pferd Husten hat, dann ist es mit 75% Wahrscheinlich-keit von dem Virus befallen. Oder noch mal anders:Ein Pferd hat Husten, dann ist es mit 75% Wahrscheinlichkeit von dem Virus befallen.
5% der Pferde, die nicht husten und gesund zu sein scheinen, sind in Wirklichkeit von dem Virus befallen. 
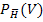= 5% = 0,05
Auch hier handelt es sich um eine bedingte Wahrscheinlichkeit, da sie sich nur auf die Pferde bezieht, die keinen Husten haben. Nicht-Husten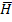 
ist deshalb die Bedingung (als Index tiefer gestellt). Die Angabe hätte auch anders formuliert werden können:Wenn ein Pferd keinen Husten hat, dann ist es mit 5% Wahrscheinlichkeit trotzdem mit dem Virus infiziert. Oder:Obwohl ein Pferd keinen Husten hat, ist es dennoch mit 5% Wahrscheinlichkeit mit dem Virus infiziert.
Hier noch einmal alle Angaben zusammengestellt:
Geg.:P(H) = 10% = 0,1 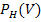= 75% = 0,75 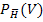= 5% = 0,05
