Bedingte Wahrscheinlichkeit

Manche Lehrer verzichten im Unterricht zwar entweder ganz auf das Zeichnen der Baumdiagramme oder sie zeichnen nur eines der beiden;davon ist jedoch absolut abzuraten, zumindest für Schüler, die mit dem Thema gerade erst beginnen! Nur mit Hilfe der Baumdiagramme kannst du  nämlich übersichtlich darstellen, was du gegeben hast, und was du berechnen sollst. Aus den Baumdiagrammen ergibt sich über die 1. Pfadregel die Formel für die bedingte Wahrscheinlichkeit von selbst. Das blinde Einsetzen in die Formel für die bedingte Wahrscheinlichkeit hilft dir vor allem dann gar nichts, wenn du aus dem Text nicht herauslesen kannst, ob und welche bedingte Wahrscheinlichkeit gegeben bzw. gesucht ist. Der Knackpunkt dieser Aufgaben ist daher die Umsetzung des Textes in die mathematische Schreibweise. Es ist nämlich für die meisten Schüler gar nicht so einfach, aus dem Text heraus zu lesen, ob eine bedingte oder etwa eine UND-Wahrscheinlichkeit vorliegt, und was im Falle einer bedingten Wahrscheinlichkeit überhaupt die Bedingung ist.

Unterscheide genau, ob eine totale, eine bedingte oder eine UND-Wahrscheinlichkeit vorliegt! Eine totale Wahrscheinlichkeit bezieht sich immer auf die Gesamtheit. Eine bedingte Wahrscheinlichkeit bezieht sich dagegen nur auf einen Teil der Gruppe. Man erkennt sie im Text an Formulierungen, welche die Wörter „wenn“ bzw. „falls“ beinhalten.

Die Wahrscheinlichkeit, dass auch B eintritt, wenn das Ereignis A eingetreten ist, schreibt man .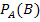

Die Wahrscheinlichkeit, dass A und B zugleich eintreten, ist dagegen .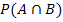

Zusammenfassung der typischen Formulierungen im Text und der entsprechenden mathematischen Schreibweise:

Formulierung im Text:	Schreibweise für die entsprechende Wahrscheinlichkeit:
Wahrscheinlichkeit, dass A eintritt. (Totale Wahrscheinlichkeit)	P(A)
Wahrscheinlichkeit, dass B eintritt. (Totale Wahrscheinlichkeit)	P(B)
A ist eingetreten. Die Wahrscheinlichkeit, dass dann B eintritt. Wenn A eingetreten ist, dass B eintritt. (Bedingte Wahrscheinlichkeit, Bedingung A)
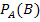B ist eingetreten. Die Wahrscheinlichkeit, dass dann A eintritt. Wenn B eingetreten ist, dass A eintritt. (Bedingte Wahrscheinlichkeit, Bedingung B)
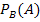Wahrscheinlichkeit, dass A und (zugleich) B eintreten. (UND-Wahrscheinlichkeit)

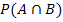Das Ganze noch einmal am obigen Beispiel:

Mögliche Formulierungen:	Mathematische Schreibweise für die entsprechende Wahrscheinlichkeit:
Die Wahrscheinlichkeit, dass eine beliebige Person ein Mann ist	P(M)
Die Wahrscheinlichkeit, dass eine beliebige Person ein Bluter ist	P(B)
Es ist ein Mann. Die Wahrscheinlichkeit, dass es dann ein Bluter ist Oder:Wenn es ein Mann ist, dass es sich dann um einen Bluter handelt. Oder:Man betrachtet nur die Männer. Von diesen sind …%  Bluter
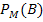Es ist ein Bluter. Die Wahrscheinlichkeit, dass es dann ein Mann ist. Oder:Wenn es ein Bluter ist, dass es sich dann um einen Mann handelt. Oder:Man betrachtet nur die Bluter. Von diesen sind …%  Männer
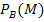Die Wahrscheinlichkeit, dass eine beliebige Person ein Mann und (zugleich) Bluter ist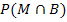

Es folgen einige weitere Beispiele, um die Thematik zu vertiefen. Versuche am besten immer selbst aus der Aufgabenstellung herauszulesen, welche Wahrscheinlichkeiten gegeben sind. Achte besonders bei den bedingten Wahrscheinlichkeiten darauf, was die Bedingung ist!

---