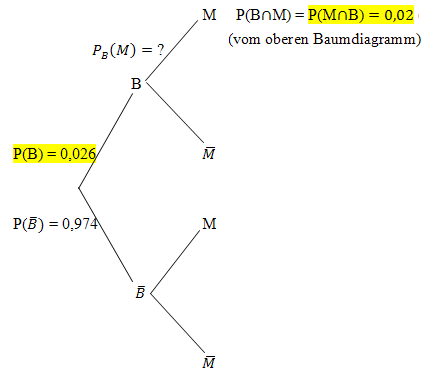
Bedingte Wahrscheinlichkeit
Ob man nun die Menge B mit der Menge M schneidet, oder ob man umgekehrt die Menge M mit der Menge B schneidet, macht keinen Unterschied. Daher kann man die UND-Wahrscheinlich-keiten, die hinter den Ästen des ersten Baumdiagramms stehen, auch wieder im zweiten Baumdiagramm verwenden. Sie finden sich aber nicht immer auf der selben Höhe wie beim ersten Baum. Die Wahrscheinlichkeit P(M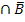 
) steht im oberen Baumdiagramm hinter dem zweiten Ast von oben, im neuen Baum müsste sie aber hinter dem dritten Ast von oben eingetragen werden, da hier die Wahrscheinlichkeit P( 
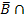M) steht. Vergleiche mit dem unten dargestellten Baumdiagramm Nr.2! Dort ist der Übersichtlichkeit wegen allerdings nur die UND-Wahrscheinlichkeit P(B 
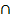M) bzw. P(M 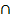B) eingetragen, da wir für die Berechnung von 
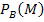die anderen UND-Wahrscheinlichkeiten nicht brauchen.
Merke:Du brauchst zur Berechnung einer bedingten Wahrscheinlichkeit immer die entsprechende totale Wahrscheinlichkeit (ganz vorne am Baum) und die UND-Wahrscheinlichkeit, die hinter dem Ast steht, an dem sich auch die gesuchte bedingte Wahrscheinlichkeit befindet!
Baumdiagramm Nr.2
Nun können wir die gesuchte bedingte Wahrscheinlichkeit 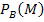ganz leicht wieder mit Hilfe der 1. Pfadregel berechnen. Diese Regel besagt ja, dass sich die UND-Wahrschein-lichkeiten ergeben, wenn man die Wahrscheinlichkeiten entlang eines Pfades miteinander multipliziert. Wendet man dies auf den obersten Ast des neuen Baumdiagramms an, ergibt sich:
P(B)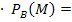 
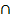P(B M)
Durch Umformen nach 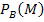erhalten wir die gesuchte bedingte Wahrscheinlichkeit:
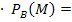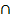P(B) P(B M) |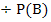 
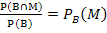
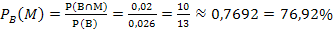
Der gesuchte Anteil der Männer unter den Blutern beträgt also 76,92%.
Damit haben wir eine Formel für die bedingte Wahrscheinlichkeit hergeleitet:
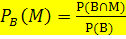
Diese Formel steht auch in der Formelsammlung bzw. Merkhilfe für das G8. Dabei wird zwar statt dem Buchstaben M der Buchstabe A verwendet, aber das dürfte für dich eigentlich kein Problem darstellen.
Warnung:Versuche nicht einfach nur stur in die Formel einzusetzen, sondern zeichne dir anfangs immer beide Baumdiagramme!
