Bedingte Wahrscheinlichkeit
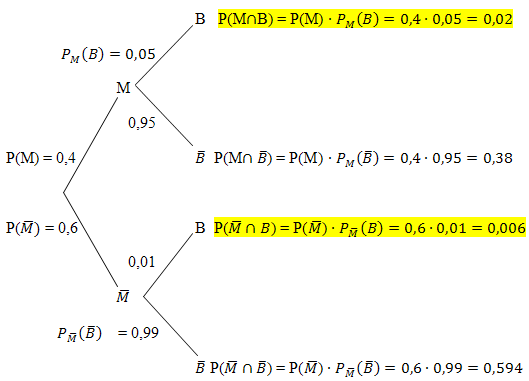
Im folgenden Baumdiagramm findest du alle nun bekannten Wahrscheinlichkeiten eingetragen.
Ebenfalls ganz leicht lassen sich die UND-Wahrscheinlichkeiten P(M 
B), P(M 
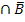), P(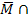 
B) und P( 
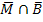) mit der 1. Pfadregel ermitteln. Die UND-Wahrscheinlichkeiten stehen immer hinter den jeweiligen Ästen des Baumdiagramms. Sie werden laut der
1. Pfadregel durch Multiplikation der Wahrscheinlichkeiten entlang eines Pfades gebildet.
Wichtig:Die UND-Wahrscheinlichkeiten beziehen sich immer auf die Gesamtheit! Verwechsle sie nicht mit den entsprechenden bedingten Wahrscheinlichkeiten!
Wenn man die UND-Wahrscheinlichkeit P(M 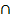B) direkt mit der bedingten Wahrscheinlich-keit 
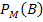vergleicht, wird der feine, aber entscheidende Unterschied deutlich:
Die UND-Wahrscheinlichkeit P(M 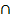B) beschreibt die Wahrscheinlichkeit, dass irgendeine Person aus der Gesamtbevölkerung ein Mann und Bluter, also ein männlicher Bluter ist. P(M 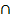B) steht daher für den Anteil der männlichen Bluter an der Gesamtbevölkerung.
Die bedingte Wahrscheinlichkeit 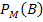beschreibt dagegen die Wahrscheinlichkeit, dass man einen Bluter erwischt, wenn man nur die Gruppe der Männer betrachtet. 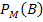steht also für der Anteil der Bluter unter den Männern.
In der Aufgabe gesucht war zuerst die totale Wahrscheinlichkeit P(B). Man berechnet sie, indem man die UND-Wahrscheinlichkeiten P(M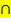 
B) und P( 
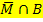) addiert. Der Anteil der männlichen Bluter P(M 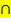B) und der Anteil der weiblichen Bluter P( 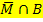) müssen schließlich zusammen wieder alle Bluter ergeben. Deshalb gilt:
P(B) = P(M 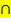B) + P( 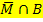) = 0,02 + 0,006 = 0,026 = 2,6%
Der Anteil der Bluter an der Gesamtbevölkerung des Landes Absurdiniens beträgt also 2,6%.
Nun müssen wir noch die zweite gesuchte Wahrscheinlichkeit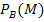 
berechnen. Zur Veranschaulichung tragen wir nun auch die Wahrscheinlichkeit 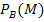in ein Baumdiagramm ein. Dazu brauchen wir nun das zweite Baumdiagramm, von dem weiter oben schon die Rede war. In diesem Baumdiagramm ist die Reihenfolge genau umgekehrt;zuerst schreiben wir B bzw. 
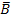, danach M bzw. 
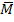. In das Baumdiagramm von oben lässt sich 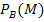nämlich nicht eintragen.
In das neue Baumdiagramm tragen wir die gerade eben berechnete totale Wahrscheinlichkeit P(B) = 0,026 und die Und-Wahrscheinlichkeit P(M 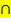B) = 0,02 ein, da wir sie zur Berechnung der bedingten Wahrscheinlichkeit 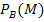benötigen.
Hinweis:Die UND-Wahrscheinlichkeiten aus dem ersten Baumdiagramm tauchen auch im zweiten Baumdiagramm auf. Die Wahrscheinlichkeiten P(B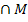 
) und P(M 
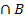) sind natürlich gleich groß, denn die Reihenfolge ist beim Schnitt zweier Mengen völlig irrelevant.
