Bedingte Wahrscheinlichkeit

Zur Übersicht noch einmal alles, was gegeben oder gesucht ist, auf einen Blick:

Geg.:

Anteil der Männer (an der Gesamtbevölkerung):     P(M) = 40% = 0,4

Anteil der Bluter unter den Männern:

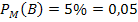
Anteil der Bluter unter den Frauen:

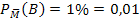
Ges.:

Anteil der Bluter (an der Gesamtbevölkerung):        P(B)

Anteil der Männer unter den Blutern:

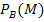
Nun zeichnen wir zwei Baumdiagramme und tragen die gegebenen Wahrscheinlichkeiten ein. Beim ersten Baumdiagramm steht an der vorderen Verzweigung M und 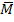und an der hinteren B und 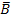, beim zweiten Baumdiagramm ist es genau anders herum, also vorne B und 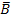, hinten M und .

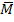Tipp:Am besten zeichnest du immer das Baumdiagramm zuerst, bei dem die totale Wahrscheinlichkeit, also die Wahrscheinlichkeit, die ganz vorne im Baumdiagramm steht, in diesem Beispiel P(M), gegeben ist.

In dieser Aufgabe ist die totale Wahrscheinlichkeit P(M) = 40% = 0,4 gegeben. Daher zeichnen wir zuerst das Baumdiagramm, das mit M und 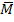beginnt.

Geg.:P(M) = 40% = 0

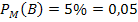
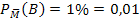
Ges.:P(B),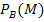

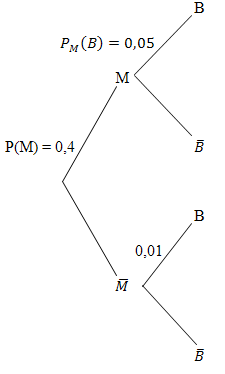
Nachdem wir die drei gegebenen Wahrscheinlichkeiten eingetragen haben, berechnen wir auch gleich die Wahrscheinlichkeiten der jeweiligen Gegenereignisse.

Zur Erinnerung:Die Wahrscheinlichkeit P( 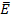) des Gegenereignisses 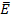(sprich:„Nicht E“) zum Ereignis E berechnet man folgendermaßen:

P( 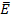) = 1 – P(E)          oder in Prozent: P( 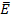) = 100% – P(E)

Da die Wahrscheinlichkeit für Mann P(M) = 0,4 ist, muss die Wahrscheinlichkeit des Gegenereignisses, also die Wahrscheinlichkeit für Frau, P( 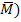= 1- 0,4 = 0,6 sein.

Man kann das auch einfach am Baumdiagramm sehen:Die Wahrscheinlichkeiten an jeder einzelnen Verzweigung ergeben zusammen immer 1. Nach dieser Methode berechnen sich auch die noch fehlenden bedingten Wahrscheinlichkeiten, also die Wahrscheinlichkeiten an den hinteren Verzweigungen. Das müsste dir an sich auch einleuchten, wenn du dir Folgendes überlegst:

Der Anteil der Bluter bei den Männern 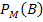beträgt laut Angabe 5% bzw. 0,05. Dann muss der Anteil der Gesunden/Nichtbluter bei den Männern 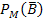wohl 95% bzw. 0,95 betragen. Zusammen müssen die Bluter und die Nichtbluter schließlich wieder 100% bzw. 1 ergeben, auch wenn man nur die Gruppe der Männer betrachtet. Bluter und Nichtbluter sind ja Gegenereignisse!

Entsprechendes gilt für die Gruppe der Frauen/Nichtmänner:Der Anteil der Bluter innerhalb der Gruppe der Frauen 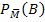beträgt laut Angabe 1% bzw. 0,01, daher muss der Anteil der Nichtbluter bei den Frauen 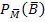natürlich 99% bzw. 0,99 sein. Die Bluter und die Nichtbluter müssen schließlich auch innerhalb der Gruppe der Frauen zusammen 100% bzw. 1 ergeben.

---