Bedingte Wahrscheinlichkeit
Um das wirklich klar zu machen, sollen diese beiden Wahrscheinlichkeiten noch einmal, aber mit anderen Worten beschrieben werden:
Laut Angabe gilt:Der Anteil der Bluter unter den Männern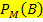 
beträgt 5%. Man könnte das auch so formulieren:Du hast einen Mann vor dir;mit einer Wahrscheinlichkeit von 5% ist er dann ein Bluter. Oder man könnte sagen:Wenn es ein Mann ist, dann ist er mit 5% Wahrscheinlichkeit ein Bluter. Egal, wie es ausgedrückt wurde, immer ist die Bedingung hier M Mann. Deshalb steht M bei der gegebenen, bedingten Wahrscheinlichkeit tiefer gesetzt.
Gesucht ist in der Aufgabe unter anderem der Anteil der Männer unter den Blutern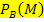 
. Das könnte man auch so formulieren:Du hast einen Bluter vor dir;mit welcher Wahrscheinlichkeit ist es dann ein Mann? Oder noch einmal anders gesagt:Wenn es ein Bluter ist, mit welcher Wahrscheinlichkeit ist es dann ein Mann? Egal, wie es ausgedrückt wurde, immer ist die Bedingung hier B Bluter. Deshalb steht B bei der gesuchten, bedingten Wahrscheinlichkeit tiefer gesetzt.
Du merkst, man muss sehr genau lesen, um diese beiden sich ähnlich anhörenden (in Wirklichkeit völlig unterschiedlichen) Wahrscheinlichkeiten nicht zu verwechseln.
Einfacher als die bedingten Wahrscheinlichkeiten sind da schon die sogenannten totalen Wahrscheinlichkeiten, wie zum Beispiel der gesuchte Anteil der Bluter P(B) insgesamt. Er bezieht sich auf die gesamte Bevölkerung, also auf die Grundgesamtheit. Wahrscheinlichkeiten oder relative Häufigkeiten, die sich auf die Gesamtheit beziehen, nennt man immer totale Wahrscheinlichkeiten. So ist z.B. der gegebene Anteil der Männer P(M) = 40% = 0,4 in diesem Land ebenfalls eine totale Wahrscheinlichkeit, weil sie sich auf die Gesamtheit bezieht.
Der gesuchte Anteil der Männer unter den Blutern ist dagegen, wie schon oben erläutert, eine bedingte Wahrscheinlichkeit, also keine totale Wahrscheinlichkeit. Man möchte ja nur wissen, wie hoch der Prozentsatz der Männer ist, wenn man nur die Gruppe der Bluter betrachtet. Die Fragestellung hätte auch lauten können:Es ist ein Bluter. Mit welcher Wahrscheinlichkeit ist es dann ein Mann? Man betrachtet daher nicht die Gesamtbevölkerung, sondern nur die Bluter. Daher ist Bluter B die Bedingung.
Anschaulich darstellen lässt sich der gesamte Sachzusammenhang mit einem Baumdiagramm, besser gesagt mit zwei Baumdiagrammen. Wenn dir jetzt der Kopf schwirrt, bitte nicht aufgeben, mit Hilfe der folgenden Baumdiagramme wird es gleich wieder einfacher!
