Bedingte Wahrscheinlichkeit

Dadurch erhält man eine Gleichung, die als einzige Unbekannte x enthält;so lässt sich x leicht berechnen:

P(P)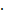

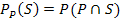
(0,93x + 0,05) 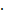0,8 = 0,98x

0,744x + 0,04 = 0,98x | – 0,744x

0,04 = 0,236x |

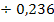
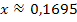
Nun wissen wir P(S) = x = 0,1695

Mit P(P) = 0,93x + 0,05 folgt:  P(P) = 0,93 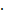0,1695 + 0,05 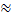0,2076

   P( 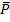) = 1 – 0,2076 = 0,7924

Aus Baum Nr.1 zweiter Ast von oben folgt:

P( 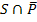) = P(S)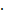

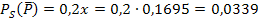
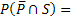P( )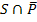

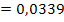
Wir verwenden dieses Ergebnis, um nun die gesuchte bedingte Wahrscheinlichkeit 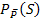zu berechnen. Dazu verwenden wir die Formel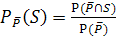

Hinweis:Diese Formel lässt sich mit dem Baumdiagramm Nr. 2 am dritten Ast von oben herleiten. Laut der 1. Pfadregel gilt:

P( |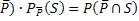

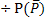
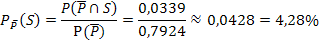
Mit einer Wahrscheinlichkeit von 4,28% ist eine Frau doch schwanger, obwohl der Test negativ war.

Diese Aufgabe war wirklich ziemlich schwer. In der 10. Klasse des G8 sind Aufgaben von diesem Schwierigkeitsgrad in Schulaufgaben oder Stehgreifaufgaben wohl kaum zu erwarten.  In einer Abiturprüfung könnte so etwas aber doch eventuell verlangt werden.

Das nächste Aufgabenbeispiel ist auch wieder für Schüler der 10.Klasse des G8 relevant. Es wirkt zwar auf den ersten Blick schwierig, ist es aber eigentlich gar nicht. Letztendlich handelt es sich wie beim 2. Bsp. um eine (allerdings etwas erweiterte) Standartaufgabe.

4. Bsp.:

Die Firma AVUC produziert Nägel in drei verschiedenen Qualitäten:

Qualität 1:normal

Qualität 2:gut

Qualität 3:sehr gut

Am häufigsten werden die billigen Nägel der Qualität 1 bestellt, daher produziert AVUC hauptsächlich Nägel dieser Qualität. 80% der gesamten Produktion umfassen daher Nägel der Qualität 1. Zur teuren Qualität 3 gehören nur 5% der Produktion von AVUC;der Rest ist Qualität 2.

---