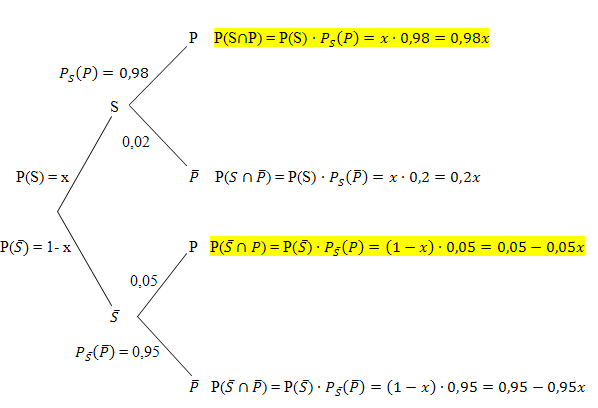Bedingte Wahrscheinlichkeit
Anders formuliert:Der Test zeigt ein negatives Ergebnis. Wie großist dann die Wahrscheinlichkeit doch schwanger zu sein? Oder noch einmal anders:Wenn der Test negativ war, wie großist dann die Wahrscheinlichkeit trotzdem schwanger zu sein? Es ist also die bedingte Wahrscheinlichkeit 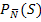 gesucht.
gesucht.
Hier noch einmal alle Angaben auf einen Blick:
Geg.: 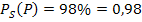
![]()
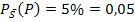
![]()
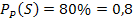
Ges.: 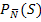
Wie bereits oben erwähnt, ist gar keine totale Wahrscheinlichkeit gegeben. Das macht diese Aufgabe deutlich schwerer als die vorherigen Aufgabenbeispiele. Sie lässt sich dennoch lösen. Es sind die beiden bedingten Wahrscheinlichkeiten 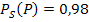 und
und 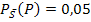 gegeben;sie stehen in dem Baumdiagramm, das als erste Verzweigung S und
gegeben;sie stehen in dem Baumdiagramm, das als erste Verzweigung S und 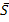 hat, an den hinteren Ästen. Vom umgekehrten Baumdiagramm, das als erste Verzweigung P und
hat, an den hinteren Ästen. Vom umgekehrten Baumdiagramm, das als erste Verzweigung P und 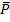 hat, ist nur eine bedingte Wahrscheinlichkeit, nämlich
hat, ist nur eine bedingte Wahrscheinlichkeit, nämlich 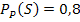 , bekannt. Daher zeichnen wir zuerst den Baum, der vorne S und
, bekannt. Daher zeichnen wir zuerst den Baum, der vorne S und 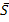 hat. Die noch unbekannte totale Wahrscheinlichkeit P(S) bezeichnen wir mit x.
hat. Die noch unbekannte totale Wahrscheinlichkeit P(S) bezeichnen wir mit x.
P(S) = x
Daher gilt für das Gegenereignis Nicht-Schwanger 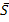 :
:
P( 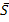 ) = 1- x
) = 1- x
Man trägt nun alle bekannten Wahrscheinlichkeiten ein und berechnet noch schnell die fehlenden bedingten Wahrscheinlichkeiten an diesem Baum. (Zur Erinnerung:Die Wahrscheinlichkeiten an jeder einzelnen Verzweigung ergeben zusammen den Wert 1.)
Die jeweiligen UND-Wahrscheinlichkeiten ergeben sich nach der 1. Pfadregel durch Multiplikation der Wahrscheinlichkeiten entlang des entsprechenden Pfades. Wir schreiben sie hinter die jeweiligen Äste des Baumdiagramms Nr1.
Baumdiagramm Nr.1
Die bedingte Wahrscheinlichkeit für „schwanger, wenn Test positiv“ 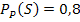 lässt sich im Baumdiagramm Nr.1 nicht eintragen;
lässt sich im Baumdiagramm Nr.1 nicht eintragen; 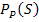 kann nur in das umgekehrte Baumdiagramm an der hinteren Verzweigung am obersten Ast eingetragen werden. Vergleiche Baumdiagramm Nr.2!
kann nur in das umgekehrte Baumdiagramm an der hinteren Verzweigung am obersten Ast eingetragen werden. Vergleiche Baumdiagramm Nr.2!
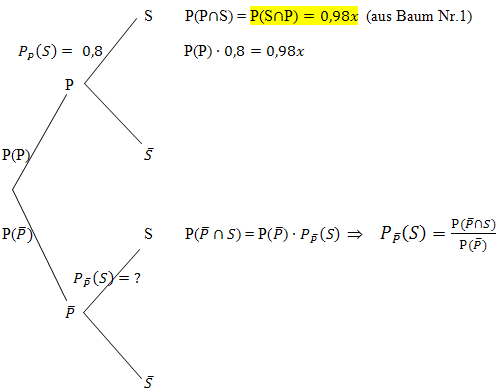
Die UND-Wahrscheinlichkeit P(S 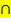 P)
P) 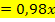 (aus Baum Nr.1) schreiben wir auch hinter den obersten Ast des Baumdiagramms Nr.2
(aus Baum Nr.1) schreiben wir auch hinter den obersten Ast des Baumdiagramms Nr.2
Baumdiagramm Nr.2
Für die totale Wahrscheinlichkeit P(P) gilt:P(P) = P(S 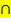 P) + P(
P) + P( 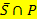 )
)
Anmerkung:„Schwanger und Positiv“ S 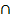 P ergibt zusammen mit „Nicht-Schwanger und Positiv“
P ergibt zusammen mit „Nicht-Schwanger und Positiv“ 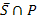 alle Positiven P.
alle Positiven P.
Aus Baum Nr.1 wissen wir: P(S 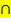 P)
P) 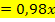 P(
P( 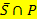 ) =
) = 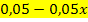
Daher gilt: P(P) = P(S 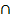 P) + P(
P) + P( 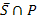 ) = 0,98x + 0,05 – 0,05x = 0,93x + 0,05
) = 0,98x + 0,05 – 0,05x = 0,93x + 0,05
Aus Baum Nr.2 (oberster Ast) können wir erkennen, dass gilt: P(P) 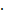
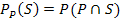
Wir setzen P(P) = 0,93x + 0,05 und die Angabe 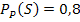 sowie
sowie 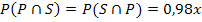 in diese Gleichung ein.
in diese Gleichung ein.