Unbestimmte Ausdrücke

Dann kannst du z. B. mit der Begründung „e-Funktion wächst stärker“ das jeweilige Ergebnis einfach hinschreiben. Allerdings reicht das nicht allen Lehrern. Manche verlangen zusätzlich eine Rechnung. Entweder man verwendet zur Berechnung unbestimmter Ausdrücke die Regeln von L´Hospital (falls im Unterricht besprochen) oder man formt die Funktion, deren Grenzwert berechnet werden soll, so um, dass man auf bekannte Grenzwerte (vergleiche Formelsammlung bzw. Merkhilfe) zurückgreifen kann. Das hängt davon ab, wie es im Unterricht vorgeführt wurde. Schau einfach in dein Mathe-Schulheft und suche nach einer Aufgabe mit einem unbestimmten Ausdruck, die dein(e) Lehrer(in) gerechnet hat. So wie es dein(e) Lehrer(in) gemacht hat, machst du es ebenfalls. Im Folgenden werden an einem konkreten Beispiel alle drei Lösungswege gezeigt, damit du dir den für dich passenden Rechen- bzw. Lösungsweg heraussuchen kannst.

Bsp.:

Gegeben ist die Funktion .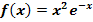

Es soll das Verhalten für 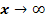untersucht werden.

Lösung:

Bei der Berechnung des Grenzwertes ergibt sich der unbestimmte Ausdruck 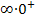. Wir können das Ergebnis auf die drei folgenden Arten herausfinden.

1. Methode:Nur mit Überlegung, ohne konkrete Rechnung

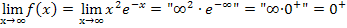
Begründung:Die e-Funktion überwiegt. Da die Null von der e-Funktion kommt, setzt sich die Null gegenüber dem Unendlich durch und es ergibt sich 0 als Ergebnis. Das Vorzeichen der 0 muss man sich gesondert überlegen: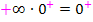

2. Methode:Mit Umformung der Funktion, so dass man letztendlich auf den bekannten Grenzwert 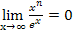kommt.

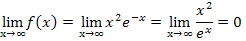
Das Vorzeichen der Null lässt sich nicht aus dem Grenzwert 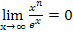, der in der Formelsammlung bzw. Merkhilfe steht, ablesen. Wenn es angegeben werden soll, muss man es sich selbst überlegen. Da aber sowohl der Zähler wegen der geraden Potenz als auch der Nenner wegen der e-Funktion immer positiv sind, ist das Vorzeichen des gesamten Bruchs und somit auch der Null natürlich ebenfalls Plus.

3. Methode:Mit der Regel von L´Hospital(Nicht auf dem Lehrplan für Gymnasien in Bayern G8. Die Regel ist aber recht einfach anzuwenden und daher sehr praktisch.)

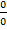Damit die Regel von L´Hospital angewendet werden kann, muss zuerst ein Bruch vorliegen, dessen Grenzwert entweder zu oder führt. Will man die Regel von L´Hospital auch auf den Fall 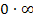anwenden, muss die Funktion vorher in einen Bruch umgewandelt werden. Das geht mit dem Potenzgesetz 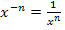. Letztendlich bedeutet dieses Potenzgesetz, dass man das Vorzeichen des Exponenten umdrehen muss, wenn man etwas aus dem Zähler in den Nenner verschieben will. Nach der Umwandlung in einen Bruch liegt dann entweder der Fall oder 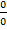vor, so dass sich nun die Regel von L´Hospital anwenden lässt. Um den Grenzwert zu berechnen, leitet man jeweils im Zähler und Nenner einzeln ab und versucht dann erneut den Grenzwert zu berechnen. Wenn sich immer noch ein unbestimmter Ausdruck, also oder 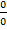ergibt, kann man auch noch einmal die Ableitung des Zählers sowie des Nenners bilden und dann wieder versuchen, den Grenzwert zu berechnen. Eventuell muss sogar ein drittes und viertes Mal abgeleitet werden, bis sich kein unbestimmter Ausdruck mehr ergibt.

Vorsicht:Bei der Regel von L´Hospital einfach die Ableitung des Zählers durch die Ableitung des Nenners teilen und davon dann den Grenzwert bestimmen, nicht die Quotientenregel verwenden! Wir suchen nämlich nicht die Ableitung der gesamten Funktion, sondern den jeweiligen Grenzwert der Funktion. Die Regel von L´Hospital ist keine Ableitungsregel, sondern eine Regel zur Berechnung von Grenzwerten mit unbestimmten Ausdrücken der Form oder .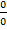

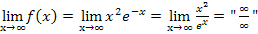
Nun kann die Regel von L´Hospital angewendet werden:Zähler ableiten und Nenner ableiten, dann erneut versuchen den Grenzwert zu ermitteln.

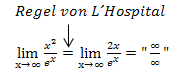
Leider hat sich auch nach der erstmaligen Anwendung der Regel von L´Hospital wieder ein unbestimmter Ausdruck ergeben. Wir müssen die Regel von L´Hospital ein zweites Mal anwenden:Noch einmal Zähler ableiten und Nenner ableiten, dann wiederum versuchen den Grenzwert zu ermitteln.

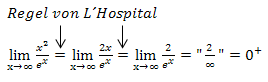
Nach zweimaliger Anwendung der Regel von L´Hospital lässt sich der Grenzwert endlich berechnen. Wir erhalten logischerweise das gleiche Ergebnis, wie schon bei den anderen beiden Methoden.

---