Polynomdivision
Der Nennergrad ist somit 1.
Der Zählergrad ist also um 1 größer als der Nennergrad;die Funktion hat eine schräge Asymptote.
Ihr Graph schmiegt sich für vom Betrag her große x-Werte beliebig nah an eine schräg verlaufende Gerade an. In einfacheren Worten:Geht x gegen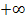 
oder gegen 
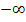, dann nähert sich der Funktionsgraph an eine schräge Gerade an. Diese Gerade heißt schräge oder schiefe Asymptote.
Um ihre Gleichung zu ermitteln, muss das Verhalten der Funktion im Unendlichen untersucht bzw. der Grenzwert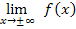 
berechnet werden. Dafür wird der Zähler der gebrochenrationalen Funktion 
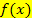durch den Nenner der Funktion geteilt und der dabei entstehende Rest weggelassen. Der Restbruch wird nämlich für x gegen 
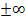sehr, sehr klein. Man sagt, er geht gegen Null, und kann deshalb bei der Berechnung der Asymptote weggelassen werden.
Wenn der Nenner der gebrochenrationalen Funktion eine Summe oder Differenz ist, muss man bei der Division des Zählers von 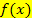durch den Nenner von 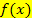eine Polynomdivision durchführen. Diese Polynomdivision geht nicht auf;es bleibt sicher ein Rest. Diesen Rest lässt du letztendlich weg und schon hast du die schräge Asymptote.
Ist der Nenner dagegen keine Summe bzw. Differenz und kann in der Form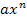 
geschrieben werden, braucht man keine Polynomdivision, sondern man teilt einfach jeden Summanden des Zählers einzeln durch den gesamten Nenner.
So lässt sich beispielsweise die Funktion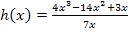 
ohne Polynomdivision umformen:
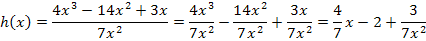
Für x gegen 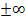wird der Bruch 
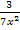unendlich klein und kann daher vernachlässigt werden. Der Graph der Funktion 
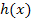nähert sich im Unendlichen immer mehr an die Gerade 
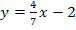an.
Die Gleichung der schrägen Asymptote von h lautet daher: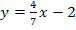
Um diese Gerade in ein Koordinatensystem einzuzeichnen, gehst du auf der y-Achse 2 nach unten, weil der y-Achsenabschnitt t hier -2 ist. Dort schneidet die Gerade die y-Achse. Von dort gehst du 7 nach rechts und 4 nach oben, weil die Steigung m hier 
ist. So erhältst du einen weiteren Geradenpunkt. Mit Hilfe dieser beiden Punkte lässt sich die Gerade zeichnen. (Mehr dazu bei:Geraden zeichnen)
Ist der Nenner einer gebrochenrationalen Funktion jedoch eine Summe bzw. Differenz, muss zwangsläufig eine Polynomdivision durchgeführt werden, um den Zähler der Funktion durch ihren Nenner zu teilen, also wenn die schräge Asymptote gesucht ist.
Um zum Beispiel die Gleichung der schrägen Asymptote 
der oben bereits erwähnten Funktion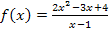 
zu ermitteln, muss vorweg der Zähler 
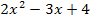durch den Nenner 
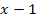geteilt werden.
