Polynomdivision

Damit ist gemeint, dass durch die Polynomdivision beispielsweise aus einem Polynom dritten Grades ein Polynom zweiten Grades wird oder aus einem Polynom vierten Grades ein Polynom dritten Grades. Man teilt den Ausdruck, der auf der linken Seite der zu lösenden Gleichung steht, durch 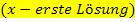. In anderen Worten:Man dreht das Vorzeichen der ersten Lösung um, wegen des Minus-Zeichens davor.

Ist beispielsweise die erratene, erste Lösung der Gleichung 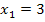, teilt man durch 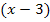. Oder wenn zum Beispiel die erste Lösung 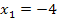ist, teilt man durch .

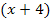·        Das Ergebnis der Polynomdivision ist ein neues Polynom, welches einen um 1 niedrigeren Grad besitzt;es wird danach wieder gleich Null gesetzt.

Wenn man mit einer Gleichung dritten Grades begonnen hat, hat man nun eine quadratische Gleichung vorliegen, die leicht z.B. mit der Mitternachtsformel oder durch Wurzelziehen zu lösen ist.

Wenn ursprünglich eine Gleichung vierten Grades gegeben war, hat man jetzt eine Gleichung dritten Grades vorliegen. Dann hilft nur eines:Es muss noch eine weitere Lösung erraten und eine zweite Polynomdivision durchgeführt werden.

Konkrete Beispiele und ausführlichere Erklärungen dazu findest du im Kapitel Gleichungen dritten und höheren Grades.

Zu 2. Polynomdivision bei gebrochenrationalen Funktionen

2a.) Zählergrad größer Nennergrad

Liegt eine gebrochenrationale Funktion vor, deren Zählergrad (höchste Potenz von x im Zähler) um genau 1 größer ist als der Nennergrad (höchste Potenz von x im Nenner), dann hat die Funktion eine schräge Asymptote. Ihre Gleichung wird meist mit Hilfe einer Polynomdivision ermittelt. Das wird im Abitur oft verlangt.

Ist der Zählergrad um mindestens 2 größer als der Nennergrad, hat die Funktion eine asymptotische Kurve. Der Graph der Funktion schmiegt sich dann beispielsweise an eine Parabel an. So etwas kommt im Abitur nur sehr selten vor. Deshalb soll das hier nur kurz erwähnt werden. (Die Rechnung funktioniert jedoch im Prinzip genauso wie bei der schrägen Asymptote – vergleiche unten – nur dass am Schluss eben keine Gerade, sondern eine Parabel oder ein Polynom höheren Grades herauskommt. Daher verwendet man dabei ebenfalls häufig eine Polynomdivision.)

Beispiel einer Funktion mit schräger Asymptote: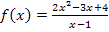

Die höchste Potenz im Zähler ist 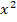. Der Zählergrad ist somit 2.

Die höchste Potenz im Nenner ist x, also .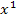

---