Polynomdivision
Weil man es nicht weiter ausrechnen kann, schreiben wir das Ganze einfach als Bruch und rechnen es eben nicht weiter aus. Wir schreiben den Rest in den Zähler des Bruchs und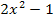 
in den Nenner. Diesen Bruch addieren wir zum bisherigen Ergebnis der Polynomdivision.
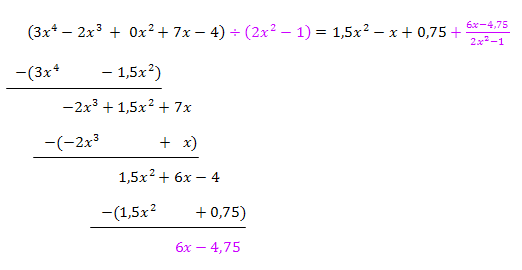
Das ist nun die komplette Lösung. Fertig!
Wofür braucht man die Polynomdivision?
Es gibt zwei völlig unterschiedliche Anwendungen der Polynomdivision, die du nicht durcheinander bringen darfst:
1. Polynomdivision beim Lösen von Gleichungen dritten und höheren Grades (Siehe auch:Grad eines Polynoms)
2. Polynomdivision bei gebrochenrationalen Funktionen mit Zählergrad größer Nennergrad, um die schräge Asymptote zu ermitteln bzw. bei gebrochenrationalen Funktionen mit Zählergrad gleich Nennergrad, um herauszufinden, ob sich der Graph von oben oder von unten an seine waagrechte Asymptote annähert
Zu 1. Polynomdivision beim Lösen von Gleichungen dritten und höheren Grades
Wenn du eine Gleichung dritten oder höheren Grades, d.h. eine Gleichung mit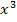 
oder sogar noch höheren Potenzen von x lösen willst, hilft oftmals eine Polynomdivision. Voraussetzung ist jedoch, dass eine Lösung bereits bekannt oder leicht zu erraten ist, weil es sich dabei um eine ganze Zahl zwischen -3 und +3 handelt.
Vorgehensweise beim Lösen von Gleichungen dritten und höheren Grades:
· Die zu lösende Gleichung wird vorweg so umgestellt, dass auf einer Seite der Gleichung eine Null zu stehen kommt. Sagen wir ´mal, dass die Null auf der rechten Seite der Gleichung steht. Alle Potenzen der Unbekannten stehen dann auf der linken Seite.
· Dann errät man die erste Lösung einer solchen Gleichung, indem man einfach nacheinander irgendwelche ganzen Zahlen von -3 bis +3 in die Gleichung einsetzt und schaut, ob sich dabei Null ergibt. Man probiert es also einfach aus.
Ein Taschenrechner, der Wertetabellen erstellen kann, ist dabei natürlich eine große Hilfe. Du brauchst dabei nur den Term, der nach dem Umstellen der Gleichung auf der linken Seite der Gleichung steht, als Funktionsgleichung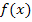 
eingeben. Als Startwert nimmst du -3 und als Endwert +3. Dann schaust du dir die Wertetabelle an und suchst einen x-Wert, für den sich 0 als zugehöriger y-Wert ergibt. Gibt es sogar mehrere x-Werte, die diese Bedingung erfüllen, kannst du dir einen davon aussuchen.
· Nun kann mit Hilfe der Polynomdivision ein Linearfaktor abgespalten werden, was dazu führt, dass der Grad des Polynoms um 1 kleiner wird.
