Polynomdivision
Immer wenn die Variable, durch die geteilt werden soll, eine höhere Potenz hat als diejenige Variable, die geteilt werden soll, bist du fertig. Dann wird die Polynomdivision beendet und der Rest, der sich nicht mehr teilen lässt, hinter das Ergebnis der Polynomdivision als Bruch geschrieben. Vor den Bruch schreibt man immer ein Plus. Im Zähler steht der Rest;im Nenner schreibt man einfach den Ausdruck hin, der in der Angabe hinter dem Geteilt-Zeichen steht, also das, durch was man eigentlich noch teilen müsste, aber eben nicht kann.
Wenn dir die Sache mit dem Rest noch nicht so ganz klar ist, schaust du dir einfach die folgenden Beispiele an. Daran solltest du es verstehen können.
Beispiel für eine Polynomdivision, die nicht aufgeht
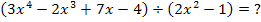
Diese Polynomdivision geht sicher nicht auf, denn die hintere Klammer ergibt Null, wenn man für x entweder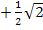 
oder 
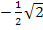einsetzt;diese Werte in die erste Klammer eingesetzt ergeben aber nicht Null. (Hinweis: 
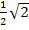ist das gleiche wie 
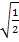;es wurde nur der Nenner rational gemacht, d.h. so umgeformt, dass der Nenner keine Wurzel mehr enthält. Siehe auch:Nenner rational machen) Du kannst das leicht selbst nachprüfen:Setze die hintere Klammer gleich Null und löse nach x auf. Das ergibt 
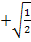und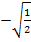 
bzw. mit rationalem Nenner 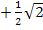und 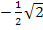. Danach setzt du diese Werte in die vordere Klammer ein. Nimm ruhig den Taschenrechner dafür! Es wird sich ein Wert ungleich Null ergeben. Die Polynomdivision kann daher nicht aufgehen;es wird ein Rest bleiben. Was du mit diesem Rest machst, soll an diesem Beispiel gezeigt werden.
Jetzt müssen wir die Polynomdivision aber erst einmal durchführen. Versuche es doch gleich selbständig, ohne vorher auf die folgende Lösung zu schauen! Beachte dabei, dass eine Potenz von x fehlt.
Hier noch einmal die Angabe:
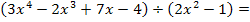
Es fehlt die zweite Potenz von x. Am besten ist es, wenn du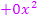 
ergänzt.
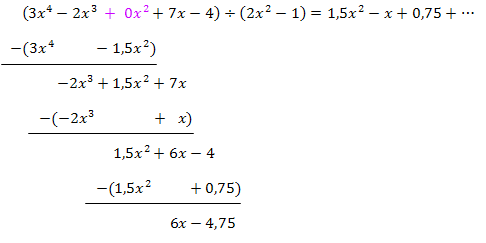
Die drei Pünktchen hinter dem Ergebnis der Polynomdivision sollen andeuten, dass hier noch etwas fehlt. Wir sind zwar mit der Polynomdivision am Ende, denn der Term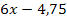 
lässt sich nicht mehr durch 
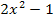teilen, ohne dass eine negative Potenz von x oder ein Bruch mit x im Nenner entsteht. Der Ausdruck 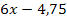bildet daher den Rest dieser Polynomdivision.
Was machen wir jetzt mit diesem Rest? Eigentlich müsste 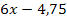noch durch 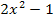dividiert werden, bloßgeht das ja nicht.
