Lineare Ungleichungen

Die Zahl -5 ist größer als die Zahl -9;diese Aussage stimmt grundsätzlich. Man sagt, die Ungleichung ist allgemein gültig. Die Lösungsmenge entspricht der jeweiligen Grundmenge. Für G = ℝ gilt beispielsweise:L = G = ℝ

Daneben gibt es aber auch lineare Ungleichungen, die zu einem Widerspruch, also zu einer falschen Aussage führen. Ergibt sich am Ende der Rechnung eine Aussage, die immer falsch ist, wie zum Beispiel 1 >3, liegt ein Widerspruch in sich vor. (Die Zahl 1 ist schließlich nicht größer als die Zahl 3.) Dann ist die Lösungsmenge unabhängig von der geltenden Grundmenge immer die leere Menge.

Beispiel einer Ungleichung, die zu einem Widerspruch führt:

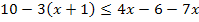
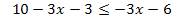
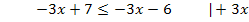
Die Variable x ist komplett herausgefallen und es hat sich eine Aussage ergeben, die grundsätzlich falsch ist. Die Zahl 7 ist schließlich nicht kleiner oder gleich der Zahl -6. Es liegt also ein Widerspruch in sich vor. Egal, was man für x einsetzt, es kommt immer etwas Falsches heraus. Es gibt also keine Zahl x, welche eingesetzt zu einer richtigen Aussage führen würde. Die Lösungsmenge ist demnach leer. Es gilt:L =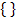

Manche Ungleichungen scheinen auf den ersten Blick nicht linear zu sein, sondern zum Beispiel quadratisch, weil zu Beginn oder während der Umformungen 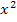vorkommt. Wenn man dann aber weiterrechnet, fällt 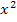komplett heraus. Erst dann lässt sich erkennen, dass es sich doch um eine lineare Ungleichung handelt.

Beispiel:

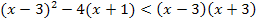
Der Ausdruck 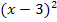wird mit Hilfe der zweiten binomischen Formel vereinfacht, der Ausdruck 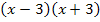mit der dritten binomischen Formel.

Zur Erinnerung:

Zweite binomische Formel: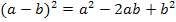

Dritte binomische Formel: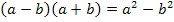

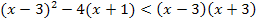
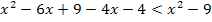
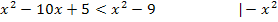
Nun erkennt man leicht, dass die Ungleichung nicht quadratisch ist, sondern linear, weil 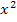komplett herausfällt.

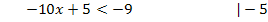
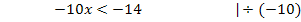
Laut Inversionsgesetz dreht sich bei der Division durch eine negative Zahl das Ungleichheitszeichen um. Es ergibt sich:

Die Lösungsmenge in der Grundmenge G = ℚ oder G = ℝ lautet:

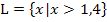oder in der Intervallschreibweise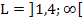

Die eckige Klammer in der Intervallschreibweise muss nach außen von der Zahl 1,4 weg zeigen, da die Zahl 1,4 ausgeschlossen werden muss. Dass 1,4 nicht mehr zur Lösungsmenge gehört, liegt daran, dass in der Ungleichung x >1,4 das Größer-Zeichen >steht und nicht das Größergleich-Zeichen 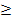. (Nur bei 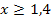wäre die Zahl 1,4 gerade noch eingeschlossen;dann würde die eckige Klammer in der Intervallschreibweise zur 1,4 hin zeigen.)

---