Faktorisierter Funktionsterm

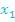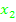Sollte es sich bei dem zu faktorisierenden Term um eine erste oder zweite binomische Formel handeln, die du jedoch nicht erkannt hast, kannst du die oben beschriebene Methode trotzdem  anwenden:Es werden sich dann allerdings für und durch die Mitternachtsformelzweimal dieselben Werte ergeben: = =

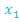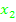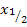
Du musst sie beide in die Formel 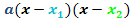einsetzen, so als wären es zwei verschiedene Zahlen. Du bekommst dadurch zweimal die gleiche Klammer, die du mit einem Quadrat zusammenfassen kannst.

Das schauen wir uns doch gleich einmal an einem konkreten Beispiel an:

3. Bsp.:  h(x) =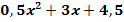

Die Funktion h(x) soll faktorisiert, also in Linearfaktoren zerlegt werden.

Wenn man zuerst die Zahl 0,5 ausklammert, wird die erste binomische Formel 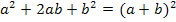erkennbar.

Zur Erinnerung:Man klammert die Zahl 0,5 aus, indem man durch 0,5 bzw. 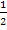teilt. Durch einen Bruch teilt man, indem man mit dem Kehrwert multipliziert, also in diesem Fall mit 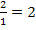multipliziert.

h(x) =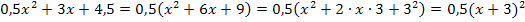

So kann man diese Funktion eigentlich am geschicktesten faktorisieren. Wenn du aber mit den binomischen Formeln auf Kriegsfußstehst, kannst du stattdessen, wie bereits erwähnt, auch die oben beschriebene Faktorisierungs-Methode anwenden:

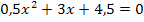(Gleich Null setzen)

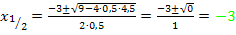(Mitternachtsformel)

h(x) = 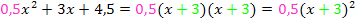(Faktorisierung)

Wir erhalten natürlich wieder dasselbe Ergebnis wie vorher, als wir die binomische Formel verwendeten.

Auch Terme mit höheren Potenzen als 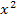lassen sich unter bestimmten Voraussetzungen faktorisieren, also als Produkt einzelner Linearfaktoren schreiben. Das musst du aber erst ab der 10. Klasse (G8) bzw. 11. Klasse FOS/BOS beherrschen.

Für Polynome dritten Grades gilt:Ein Term der Form 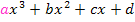kann nur dann in der Form 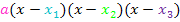geschrieben werden, wenn sich aus der Gleichung 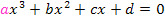drei Lösungen 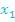, 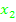und 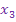ergeben. Hat die Gleichung eine einfache Lösung 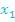und eine doppelte Lösung 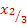(d.h. die Lösungen 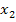und 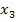fallen zusammen, weil sie gleich sind), dann lässt sich der Term 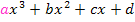in der Form 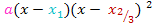schreiben. Hat die Gleichung 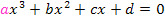allerdings nur eine einzige Lösung, kann nur ein Linearfaktor abgespalten werden. Es verbleibt ein quadratischer Faktor, der sich nicht weiter zerlegen lässt. Man erhält den quadratischen Faktor mittels Polynomdivision durch den Linearfaktor. Ausführlichere Erklärungen und konkrete Beispiele dazu findest du im Kapitel Polynomfunktionen / Ganzrationale Funktionen dritten und höheren Grades. Dort findest du ebenfalls Beispiele zur Faktorisierung von Polynomen vierten und noch höheren Grades.

---