Faktorisierter Funktionsterm

Die einzelnen Linearfaktoren erhältst du dann, indem du jeweils ( x – Lösung der Gleichung) schreibst. Damit ist gemeint, dass du in der Klammer hinter x jeweils die Lösung der Gleichung mit umgedrehtem Vorzeichen schreiben sollst.

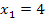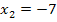Hat die Gleichung, die du durch das Nullsetzen erhalten hast, beispielsweise die beiden Lösungen und , dann gibt es zwei Linearfaktoren. Der erste Linearfaktor muss die Form 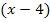haben und entsprechend der zweite die Form 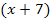. Nun nimmst du noch die Zahl, die in der nicht-faktorisierten Form vor der höchsten Potenz von x steht, und schreibst sie vor die beiden Linearfakoren. Wir nennen diese Zahl hier einfach ´mal a, weil wir ja momentan kein konkretes Beispiel vorliegen haben. (a ist normalerweise natürlich eine konkrete Zahl und natürlich nicht gerade Null.) Du multiplizierst also a mit den Linearfaktoren. So erhältst du die faktorisierte Funktionsgleichung f(x) = 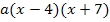. Falls dir das im Moment noch nicht wirklich klar sein sollte, ist das gar nicht schlimm. Schau dir einfach die folgenden konkreten Beispiele an. Daran wird alles noch einmal ausführlich erklärt.

2. Bsp.: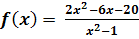

Die Funktion soll vollständig, also sowohl im Zähler als auch im Nenner, faktorisiert werden.

Lösung:

Fangen wir mit dem Einfacheren an, dem Nenner:Der Nenner lässt sich ganz leicht mit Hilfe der dritten binomischen Formel faktorisieren.

Zur Erinnerung:

Dritte binomische Formel: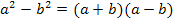

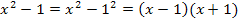
Nun zu dem schwierigeren Zähler:Im Zähler kann man entweder zuerst die Zahl 2 ausklammern und danach den Satz von Vietaanwenden oder nach folgender Methode vorgehen:

·        Gleich Null setzen: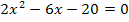 

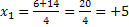
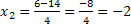
·        Mitternachtsformel:   

Da es zwei Lösungen gibt, gibt es auch zwei Linearfaktoren. Sie lauten in diesem Fall 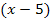   und 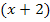. Hinter dem x in der Klammer steht jeweils eine der Lösungen aber mit umgedrehtem Vorzeichen.

·        Faktorisierung:

Nun kann die Funktion vollständig faktorisiert geschrieben werden:

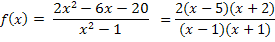
Warum das so ist, musst du nicht unbedingt wissen. Dass die Umformung tatsächlich richtig ist, kannst du aber ganz einfach nachprüfen, indem du die faktorisierte Form der Funktion ausmultiplizierst;es wird wieder die ursprüngliche Funktionsgleichung herauskommen!

Besser wäre es natürlich schon, wenn du verstehst, warum du auf die oben gezeigte Art einen Funktionsterm faktorisieren kannst. Wenn du also doch wissen möchtest, warum die beschriebene Methode zur Zerlegung 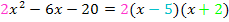richtig sein muss, überlege dir Folgendes:

---