Differenzierbarkeit/Differenzierbare Funktion
Mit f´(x) ist die erste Ableitung der Funktion f, also ihre Steigung gemeint.
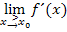 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen  von rechts von f Strich von x“
von rechts von f Strich von x“
Das Größer-Zeichen über dem Pfeil zwischen x und  bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle  von rechts. x ist also ein klein wenig größer als der feste Zahlenwert
von rechts. x ist also ein klein wenig größer als der feste Zahlenwert  . Man nähert sich daher von rechts an die „Problemstelle“
. Man nähert sich daher von rechts an die „Problemstelle“  an.
an.
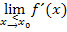 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen  von links von f Strich von x“
von links von f Strich von x“
Das Kleiner-Zeichen über dem Pfeil zwischen x und  bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle  von links. x ist also etwas kleiner als der feste Zahlenwert
von links. x ist also etwas kleiner als der feste Zahlenwert  . Man nähert sich daher von links an die „Problemstelle“
. Man nähert sich daher von links an die „Problemstelle“  an.
an.
Oben gezeigte Definition noch einmal in Worten:Ist das Ergebnis des Limes von rechts der ersten Ableitung gleich dem Limes von links, ist eine stetige Funktion an der Stelle 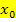 differenzierbar, d.h. sie hat dort keinen Knick. Die Teilfunktionen einer teilweise definierten Funktion gehen „weich“ ineinander über.
differenzierbar, d.h. sie hat dort keinen Knick. Die Teilfunktionen einer teilweise definierten Funktion gehen „weich“ ineinander über.
Beispiele:
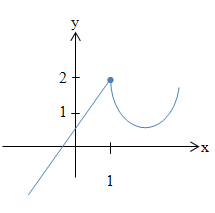 |
Die Funktion ist an der Stelle 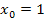 stetig (keine Sprungstelle), aber nicht differenzierbar (Knick). stetig (keine Sprungstelle), aber nicht differenzierbar (Knick). |
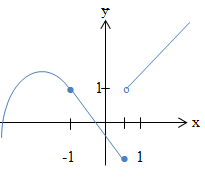 |
Die Funktion ist an der Stelle 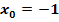 stetig (keine Sprungstelle) und differenzierbar (kein Knick), aber an der Stelle stetig (keine Sprungstelle) und differenzierbar (kein Knick), aber an der Stelle  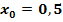 nicht stetig (Sprungstelle) und daher auch nicht differenzierbar. nicht stetig (Sprungstelle) und daher auch nicht differenzierbar. |
Die rechnerische Untersuchung der Differenzierbarkeit, also die Berechnung von 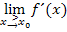 und
und 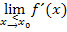 , geschieht entweder mit der h-Methode oder einfacher durch Einsetzen von
, geschieht entweder mit der h-Methode oder einfacher durch Einsetzen von  in die erste Ableitung sowohl der einen als auch der anderen Teilfunktion einer teilweise definierten Funktion. Nachdem die Stetigkeit an der Stelle
in die erste Ableitung sowohl der einen als auch der anderen Teilfunktion einer teilweise definierten Funktion. Nachdem die Stetigkeit an der Stelle 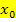 nachgewiesen wurde, leitet man also die einzelnen Teilfunktionen mit Hilfe der Ableitungsregeln ab. Dann setzt man
nachgewiesen wurde, leitet man also die einzelnen Teilfunktionen mit Hilfe der Ableitungsregeln ab. Dann setzt man 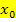 nacheinander in die einzelnen Ableitungen der beiden Teilfunktionen, die an der Stelle
nacheinander in die einzelnen Ableitungen der beiden Teilfunktionen, die an der Stelle 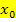 zusammenstoßen, ein. Ergibt sich dabei zweimal das gleiche Ergebnis, ist die Funktion an der Stelle
zusammenstoßen, ein. Ergibt sich dabei zweimal das gleiche Ergebnis, ist die Funktion an der Stelle 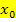 differenzierbar.
differenzierbar.
Beispiel: f(x) = 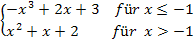
Es soll überprüft werden, ob die Funktion f an der Stelle 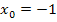 differenzierbar ist.
differenzierbar ist.
1. Schritt: Untersuchung der Stetigkeit
Es müssen die Grenzwerte der Funktion f(x) für 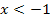 und
und 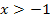 sowie der Funktionswert f(-1) berechnet werden.
sowie der Funktionswert f(-1) berechnet werden.
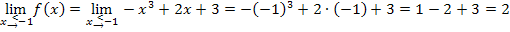
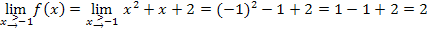
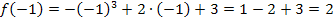
Es ergibt sich immer das gleiche Ergebnis. Daher ist die Funktion f an der Stelle 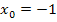 stetig.
stetig.
2. Schritt: Untersuchung der Differenzierbarkeit
Die Funktion wird zuerst abgeleitet, damit danach die Grenzwerte der Ableitung für 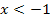 und
und 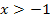 berechnet werden können.
berechnet werden können.
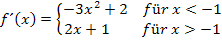
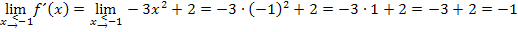
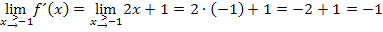
Es ergibt sich zweimal der selbe Wert. Die Funktion hat also von links und von rechts bei 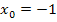 die gleiche Steigung. Daher ist die Funktion f an der Stelle
die gleiche Steigung. Daher ist die Funktion f an der Stelle 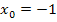 differenzierbar. Der Graph
differenzierbar. Der Graph 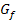 hat keinen Knick;er verläuft „weich“.
hat keinen Knick;er verläuft „weich“.
Mehr zum Thema Differenzierbarkeit findest du im Bereich Analysis im Kapitel Stetigkeit und Differenzierbarkeit.
- Page 2 of 2
- « Previous
- 1
- 2
- Next »

