Binom/Binomische Formeln

Bsp.:  Vereinfache den Term T(x) = 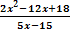soweit möglich!

Lösung:

Zuerst klammern wir im Zähler den Faktor 2 und im Nenner den Faktor 5 aus. Im Zähler kann dann die zweite Binomische Formel angewendet werden. Nun liegt sowohl im Zähler als auch im Nenner ein Produkt vor und wir dürfen kürzen.

T(x) =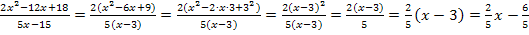

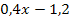
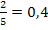T(x) = ,da  und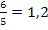

An diesem Beispiel kannst du sehen, dass die Binomische Formel oft nicht so leicht zu erkennen ist. Erkennt man sie man sie jedoch nicht, kann man gar nicht weiter rechnen! Daher ist es absolut unerlässlich, die Binomischen Formeln gut zu können. Du wirst sie in den verschiedensten Zusammenhängen immer wieder brauchen. Nun wirst du dir vielleicht denken:„ Dass da in dem Term T(x) ein Binom versteckt ist, das erkenne ich alleine nie!“ Das ist aber nur Übungssache. Am besten wandelst du zuerst einige Binome von der Produkt-Seite in die Summen/Differenzen-Seite um. Erst wenn das klappt, übst du es umgekehrt. Danach kannst du es probieren, Aufgaben zu lösen, bei denen zuerst ausgeklammert werden muss, bevor dann ein Binom verwendet werden kann.

Vor einem extrem häufigen Fehler sei noch einmal extra gewarnt:

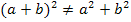
bzw.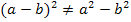   

Wir haben schließlich oben hergeleitet, dass gilt:

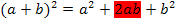bzw.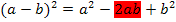   

Vergiss das gemischte Glied 2ab nicht und pass, vor allem bei der zweiten Binomischen Formel, auf die Vorzeichen auf!

Steht in der Klammer jedoch an Stelle von Plus oder Minus ein Mal-Punkt, dann darf man jeden Faktor einzeln quadrieren. Dann liegt allerdings auch keine Binomische Formel vor.

Es gilt:

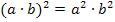
Mehr zu den Binomischen Formeln findest du im Bereich Algebra im Kapitel Binomische Formeln.

---