Binom/Binomische Formeln

Vielen Schülern fällt das Faktorisieren mit Hilfe der Binomischen Formeln zu Beginn schwer. Um eine Binomische Formel in ihrer Summen- bzw. Differenzen-Form zu erkennen, überlegt man sich zuerst, ob zwei verschiedene Quadratzahlen bzw. Variablen zum Quadrat vorhanden sind. Dann fragt man sich, welches Binom vorliegen könnte. Ohne gemischtes Glied kann nur noch die dritte Binomische Formel vorliegen. Vorsicht:Zwischen den beiden Quadraten muss ein Minus stehen, damit es wirklich das dritte Binom 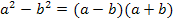ist! ist 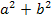nämlich keine Binomische Formel! Die erste oder zweite Binomische Formel kann nur dann vorliegen, wenn zusätzlich zu den Quadraten bzw. Quadratzahlen auch ein gemischtes Glied vorhanden ist. Steht vor dem gemischten Glied ein Plus, kommt nur noch die erste Binomische Formel in Frage. Steht vor dem gemischten Glied ein Minus, kann dagegen nur die zweite Binomische Formel vorliegen. Ob es nun wirklich die erste bzw. zweite Binomische Formel ist, hängt vom gemischten Glied ab. Das kontrollierst du am besten nachträglich. D.h. du tust so als wäre es ein Binom und formst  einfach mal – ohne Rücksicht auf das gemischte Glied -  in die Form 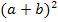bzw. 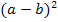um. Danach bildest du mit der nun von dir hingeschriebenen Binomischen Formel selbst das gemischte Glied 2ab und vergleichst es mit dem ursprünglich vorliegenden Term. Stimmt das gemischte Glied, liegt tatsächlich ein Binom vor und die Umformung ist richtig. Ist das gemischte Glied falsch, liegt keine Binomische Formel vor. Der Ausdruck kann dann nicht auf die Form 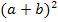bzw. 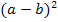gebracht werden. Du streichst daher deine Umformung einfach wieder durch. Der Term kann dann, zumindest mit den Binomischen Formeln, nicht faktorisiert werden.

Beispiele: Summe bzw. Differenz    Produkt

1. Binom:

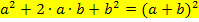
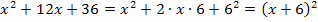
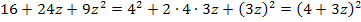
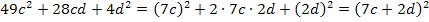
Nur für Schüler, die Wurzeln bereits gelernt haben:

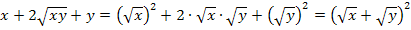
2. Binom:

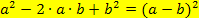
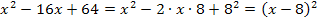
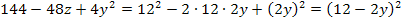
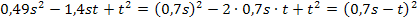
Nur für Schüler, die Wurzeln bereits gelernt haben:

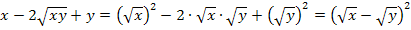
3. Binom: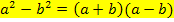   

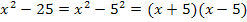
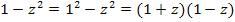
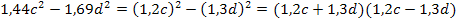
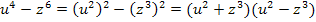
Nur für Schüler, die Wurzeln bereits gelernt haben:

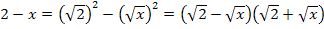
Wie gesagt, kann nicht jede Summe oder Differenz mit einer der Binomischen Formeln in ein Produkt umgewandelt werden. Die Kunst besteht also darin zu erkennen, ob überhaupt eine Binomische Formel vorliegt und wenn ja, welche. Manchmal muss auch zuerst ausgeklammert werden, bevor eine Binomische Formel angewendet werden kann. Außerdem steht in den meisten Fällen in der Aufgabenstellung gar nicht, dass man faktorisieren muss, sondern es heißt meistens nur, dass man soweit möglich vereinfachen soll. Man muss also selbst auf die Idee kommen, dass man eine Binomische Formel anwenden kann, damit man danach dann beispielsweise kürzen kann.

---