Bestimmtes Integral

In einem zweiten Schritt werden dann die Grenzen bei F(x) eingesetzt:Zuerst die obere Grenze für x eingesetzt, dann minus die untere Grenze eingesetzt.

Beispiel: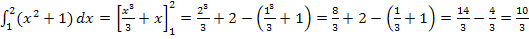

Dir ist nicht klar, wie man auf den Ausdruck in der eckigen Klammer gekommen ist? Der Ausdruck 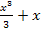ist durch Integration der Funktion 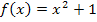entstanden. 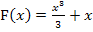ist eine Stammfunktion zu 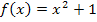. Man erhält eine Stammfunktion bei Funktionen der Form 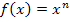, indem man zum Exponenten 1 dazu zählt und außerdem durch den neuen Exponenten teilt. Die Integration ist quasi das Gegenteil des Ableitens. Kontrolle:Die Stammfunktion, also der Ausdruck in den eckigen Klammern, muss abgeleitet wieder 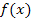ergeben, also die Funktion, die hinter dem Integralzeichen steht.

Unterschied zwischen bestimmtem und unbestimmtem Integral:

Ein bestimmtes Integral hat immer zwei Grenzen a und b. (Die Grenzen sind natürlich konkrete Zahlen.) Im Gegensatz dazu hat ein Unbestimmtes Integralkeine Grenzen.

Das unbestimmte Integral 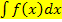entspricht der Menge aller Stammfunktionen 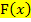einer Funktion .

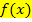Mehr dazu im Bereich Analysis im Kapitel Einführung in die Integralrechnung.

---