Punktprobe: Liegt der Punkt P in der Ebene E?
Geg.: P( 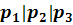 ) E:
) E: 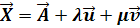
Liegt die Ebene E in Parameterform vor und du sollst überprüfen, ob der Punkt P in der Ebene E liegt, machst du die sogenannte Punktprobe. Du kennst vermutlich bereits die Punktprobe, ob ein Punkt auf einer Gerade liegt. Vergleiche dazu Punktprobe:Liegt der Punkt P auf der Gerade g? Bei der Überprüfung, ob ein Punkt auf einer Ebene liegt, die in Parameterform gegeben ist, gehst du ähnlich vor:
Ø Punkt für x in die Parametergleichung der Ebene einsetzen
Ø Jede der drei Zeilen als einzelne Gleichung schreiben
Ø Vorerst eine der drei Gleichungen weglassen und mit den verbleibenden zwei Gleichungen die beiden Parameter berechnen
Ø In die zuerst weggelassene Gleichung die ermittelten Werte für beide Parameter zugleich einsetzen
Ø Ergibt sich eine wahre Aussage (z.B. 3 = 3) liegt der Punkt in der Ebene, ergibt sich dagegen ein Widerspruch (z.B. 2 = 6) liegt der Punkt nicht in der Ebene.
Anmerkung:Es dauert relativ lange, mit der Parameterform einer Ebene die Punktprobe durchzuführen. (Das wirst du gleich am folgenden Beispiel sehen.) Wenn du bereits die Koordinatenform von Ebenen gelernt hast, empfiehlt es sich, von der Parameterform in die Koordinatenform der Ebene umzurechnen. Mit der Koordinatenform ist es ganz einfach zu überprüfen, ob ein Punkt in der Ebene liegt. Siehe Koordinatenform!
1. Bsp.: Überprüfe, ob die Punkte P(-7| 8| -11) und Q(2| 3| -1) in der Ebene E liegen!
![]() E:
E: 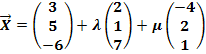
Lösung:
Wie oben beschrieben machen wir die Punktprobe nacheinander mit beiden Punkten. wir beginnen mit Punkt P.
P  E ?
E ?![]()
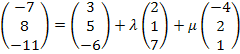
![]() I.
I. 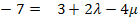
![]() II.
II. 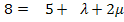
![]() III.
III. 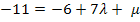
Durch das Einsetzen von P für X und das Aufteilen in drei einzelne Gleichungen, erhalten wir ein überbestimmtes Gleichungssystem, d.h. drei Gleichungen für nur zwei Unbekannte, also eigentlich eine Gleichung zu viel. Wie bereits in der Anleitung für die Punktprobe beschrieben, lassen wir deshalb vorerst eine der drei Gleichungen weg. Wir entscheiden uns dafür, die Gleichung III. erst einmal wegzulassen, und ermitteln dann nur mit den verbliebenen Gleichungen I. und II. die beiden Parameter 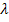 und
und 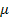 . Dafür kann sowohl das Additionsverfahren als auch das Einsetzungsverfahren verwendet werden;das ist Geschmackssache. Hier soll nur das Additionsverfahren vorgeführt werden. Es soll der Parameter
. Dafür kann sowohl das Additionsverfahren als auch das Einsetzungsverfahren verwendet werden;das ist Geschmackssache. Hier soll nur das Additionsverfahren vorgeführt werden. Es soll der Parameter 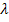 eliminiert werden. Dazu multiplizieren wir die Gleichung II. mit dem Faktor 2 und subtrahieren das Ergebnis von I.
eliminiert werden. Dazu multiplizieren wir die Gleichung II. mit dem Faktor 2 und subtrahieren das Ergebnis von I.
I. 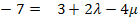
![]() II.
II. 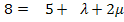 |
| 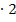
![]() I.
I. 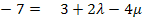
![]()
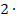 II.
II. 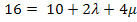
![]() I.
I. 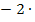 II.
II. 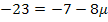
![]() |
| 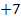
![]()
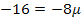
![]() |
| 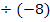
![]()
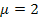
Nun setzt man 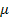 in eine der Gleichungen I. oder II. ein, um
in eine der Gleichungen I. oder II. ein, um 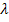 zu erhalten. (Achtung:Auf keinen Fall darf
zu erhalten. (Achtung:Auf keinen Fall darf 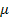 in die vorerst weggelassene Gleichung III. eingesetzt werden, um
in die vorerst weggelassene Gleichung III. eingesetzt werden, um 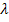 zu berechnen! III. darf erst zur Kontrolle am Ende der Rechnung benützt werden.) Wir setzen nun
zu berechnen! III. darf erst zur Kontrolle am Ende der Rechnung benützt werden.) Wir setzen nun 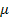 in die Gleichung II. ein. Man hätte natürlich genauso gut I. verwenden können.
in die Gleichung II. ein. Man hätte natürlich genauso gut I. verwenden können.
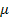 in II.
in II.![]()
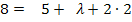
![]()
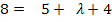
![]()
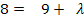
![]() |
| 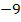
![]()
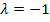
Nachdem jetzt 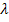 und
und 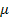 ermittelt sind, folgt die Kontrolle. Man setzt dazu
ermittelt sind, folgt die Kontrolle. Man setzt dazu 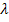 und
und 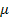 gleichzeitig in die zuvor weggelassene Gleichung III. ein. Wenn sich eine wahre Aussage ergibt, liegt der Punkt in der Ebene.
gleichzeitig in die zuvor weggelassene Gleichung III. ein. Wenn sich eine wahre Aussage ergibt, liegt der Punkt in der Ebene.
Kontrolle: 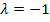 und
und 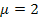 in III.
in III. 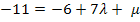
![]()
![]()
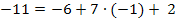
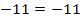 (wahr)
(wahr)![]()
 P
P  E
E
Da sich bei der Kontrolle eine wahre Aussage ergibt, liegt P in der Ebene E.
Entsprechend verfahren wir nun mit dem zweiten Punkt Q.
Hier noch einmal die Angaben:
Q(2| 3| -1)![]() E:
E: 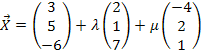
Q  E ?
E ?![]()
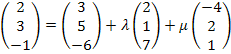
![]() I.
I. 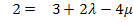
![]() II.
II. 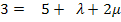
![]() III.
III. 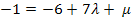
Wir lassen wieder III. vorerst weg und berechnen mit I. und II. die beiden Parameter 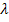 und
und 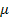 .
.
I. 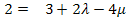
![]() II.
II. 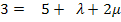 |
| 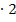
![]() I.
I. 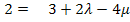
![]()
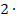 II.
II. 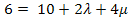
![]() I.
I. 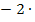 II.
II. 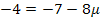
![]() |
| 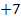
![]()
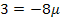
![]() |
| 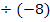
![]()
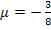
Nun wird 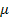 in I. oder II. eingesetzt, um
in I. oder II. eingesetzt, um 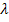 zu ermitteln. Wir nehmen Gleichung II.
zu ermitteln. Wir nehmen Gleichung II.
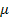 in II.
in II.![]()
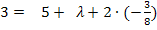
![]()
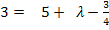
![]()
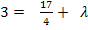
![]() |
| 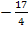
![]()
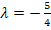
Als Letztes kommt wieder die Kontrolle, d.h. beide Parameter in die vorher weggelassene Gleichung einsetzen.
Kontrolle: 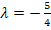 und
und 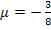
![]() in III.
in III. 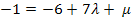
![]()
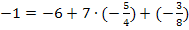
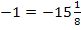 (Widerspruch)
(Widerspruch)  Q
Q  E
E
Da sich bei der Kontrolle ein Widerspruch ergibt, liegt Q nicht in der Ebene E.
2. Bsp.:Die Punkte A(-7| a| 10) und B(b| b – 3| 3b) liegen in der Ebene E.
Ermittle die Koordinaten der Punkte A und B nur mit Hilfe der Parameterform der Ebene E (ohne Umrechnung in die Koordinatenform der Ebene)!
E: 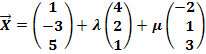
Lösung:
Der Punkt A(-7| a| 10) soll in der Ebene E liegen. Um a zu berechnen, setzen wir die Koordinaten von A für X in die Ebenengleichung ein. Dann schreiben wir jede Zeile als einzelne Gleichung. So erhalten wir ein Gleichungssystem, bestehend aus drei Gleichungen und den drei Unbekannten a, 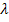 und
und 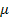 . Es lässt sich beispielsweise mit dem Additionsverfahren lösen. (Wenn es dir leichter fällt, kannst du natürlich auch das Einsetzungsverfahren verwenden. Das dauert aber länger und ist deshalb nicht wirklich empfehlenswert.)
. Es lässt sich beispielsweise mit dem Additionsverfahren lösen. (Wenn es dir leichter fällt, kannst du natürlich auch das Einsetzungsverfahren verwenden. Das dauert aber länger und ist deshalb nicht wirklich empfehlenswert.)
A in E:
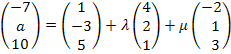
I. 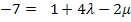 |
| 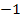
II.![]()
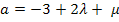
III. 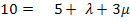 |
| 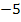
I. 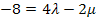
II.![]()
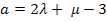
III. 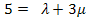
In den Gleichungen I. und III. kommt a nicht vor, sondern nur die Unbekannten 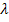 und
und 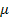 . Das macht uns das Lösen des Gleichungssystems wesentlich leichter. Wir eliminieren nun außerdem
. Das macht uns das Lösen des Gleichungssystems wesentlich leichter. Wir eliminieren nun außerdem 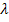 , indem wir die Gleichung III. mit dem Faktor 4 multiplizieren und dann von I. subtrahieren. (Weil in I. bereits die Zahl 4 vor
, indem wir die Gleichung III. mit dem Faktor 4 multiplizieren und dann von I. subtrahieren. (Weil in I. bereits die Zahl 4 vor 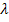 steht, multiplizieren wir III. mit dem Faktor 4. Durch Subtraktion der beiden Gleichungen fällt dann
steht, multiplizieren wir III. mit dem Faktor 4. Durch Subtraktion der beiden Gleichungen fällt dann 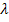 weg und
weg und 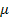 kann berechnet werden.) Wir ermitteln also zuerst mit den Gleichungen I. und III. die Unbekannten
kann berechnet werden.) Wir ermitteln also zuerst mit den Gleichungen I. und III. die Unbekannten 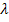 und
und 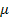 . Danach setzen wir die ermittelten Werte für
. Danach setzen wir die ermittelten Werte für 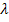 und
und 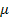 in II. ein, um a zu berechnen.
in II. ein, um a zu berechnen.
I. 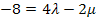
III. 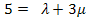
![]() |
| 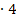
I. 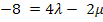
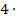 III.
III. 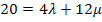
I. – 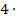 III.
III. 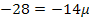 |
| 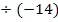
![]()
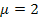
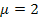 in III.
in III. 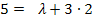
![]()
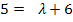
![]()
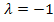
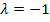 und
und 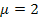 in II.
in II. 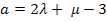
![]()
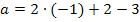
![]()
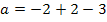

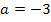
Der Punkt A hat die Koordinaten A(-7| -3| 10).
Nun verfahren wir entsprechend mit Punkt B(b| b – 3| 3b). Wir setzen ihn für x in die Gleichung der Ebene E ein.
Hier noch einmal die Angabe: E: 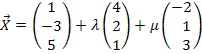
B in E:
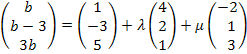
I. 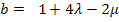
II. 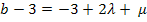 |+ 3
|+ 3
III. 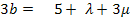
I. 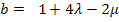
II. 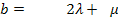
III. 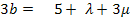
Es liegt ein Gleichungssystem, bestehend aus drei Gleichungen und den drei Unbekannten b, 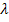 und
und 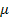 vor. Es lässt sich beispielsweise mit dem Additionsverfahren lösen. (Wenn es dir leichter fällt, kannst du natürlich auch das Einsetzungsverfahren verwenden. Das dauert aber länger und ist deshalb nicht wirklich empfehlenswert.) Es bietet sich an, die beiden Gleichungen I. und II. zu subtrahieren, um b zu eliminieren. So entsteht eine Gleichung, die nur noch
vor. Es lässt sich beispielsweise mit dem Additionsverfahren lösen. (Wenn es dir leichter fällt, kannst du natürlich auch das Einsetzungsverfahren verwenden. Das dauert aber länger und ist deshalb nicht wirklich empfehlenswert.) Es bietet sich an, die beiden Gleichungen I. und II. zu subtrahieren, um b zu eliminieren. So entsteht eine Gleichung, die nur noch 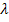 und
und 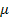 enthält. Um
enthält. Um 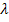 und
und 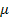 berechnen zu können, brauchen wir aber noch eine weitere Gleichung, die kein b mehr enthält. Man erhält so eine Gleichung, indem man beispielsweise die Gleichung II. mit dem Faktor 3 multipliziert und dann Gleichung III. davon subtrahiert.
berechnen zu können, brauchen wir aber noch eine weitere Gleichung, die kein b mehr enthält. Man erhält so eine Gleichung, indem man beispielsweise die Gleichung II. mit dem Faktor 3 multipliziert und dann Gleichung III. davon subtrahiert.
I. – II.![]()
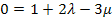 Wir nennen diese Gleichung IV.
Wir nennen diese Gleichung IV.
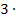 II.
II. ![]()
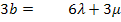
III.![]()
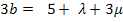
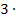 II. – III.
II. – III. 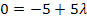
![]() |+ 5
|+ 5
![]()
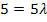
![]() |
| 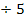
![]()
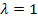
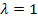 in IV.
in IV. 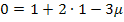
![]()
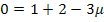
![]()
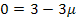
![]() |
| 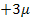
![]()
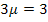
![]()
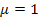
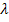 und
und 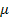 in I.
in I. 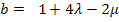
![]()
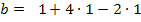
![]()
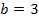
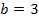 in B(b| b – 3| 3b)
in B(b| b – 3| 3b)  B(3| 0| 9)
B(3| 0| 9)
Anmerkung:Man hätte diese Aufgabe natürlich wesentlich einfacher lösen können, wenn die Ebene in ihre Koordinatenform umgerechnet hätte werden dürfen. Es sollte an diesem Beispiel nur gezeigt werden, wie das auch ohne Verwendung der Koordinatenform funktioniert. Im Normalfall rechnest du die Ebene aber besser um und setzt dann die Punkte einfach in die Koordinatenform der Ebene ein. Wie das genau gemacht wird, kannst du im Kapitel Koordinatenform einer Ebene nachlesen.

