Parameterform einer Ebene
Du kennst sicherlich die Parameterform einer Geraden:
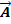stellt dabei den Ortsvektor des Aufpunkts und 
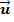den Richtungsvektor der Geraden dar. 
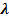ist der sogenannte Parameter. Geraden werden immer mit kleinen lateinischen Buchstaben benannt, z.B. Gerade g oder Gerade h.
Eine Ebene kann ebenfalls durch eine Parametergleichung beschrieben werden. Die Parametergleichung einer Ebene enthält allerdings neben dem Ortsvektor des Aufpunkts zwei Richtungsvektoren, welche die Ebene aufspannen. Ebenen werden immer mit großen lateinischen Buchstaben bezeichnet, z.B. Ebene E oder Ebene F.
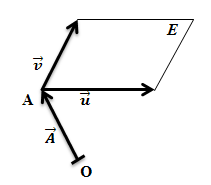
Anmerkungen zur Skizze:Die Ebene E ist hier durch das Parallelogramm angedeutet. Eine Ebene hat natürlich keine Ränder, sie geht in alle Richtungen weiter! Auch der Aufpunkt A der Ebene liegt eigentlich irgendwo im Inneren der Ebene und nicht an einer Ecke;eine Ebene hat ja gar keine Ecken! Diese Art der zugegebenermaßen nicht ganz korrekten Darstellung wurde nur ihrer Einfachheit wegen gewählt. So kannst auch du selber schnell Skizzen zeichnen, die dir z.B. beim Aufstellen von Ebenengleichungen helfen. Übe das Zeichnen von einfachen Skizzen! Es wird dir vor allem später, wenn die Aufgaben komplexer werden, wirklich helfen. Die Lage des Ursprungs ist bei solchen einfachen Skizzen praktisch frei wählbar. Nur einzeichnen muss man den Ursprung O unbedingt, denn ohne Ursprung lässt sich der Ortsvektor des Aufpunkts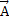 
(=Vektor vom Ursprung zum Aufpunkt A) nicht darstellen.
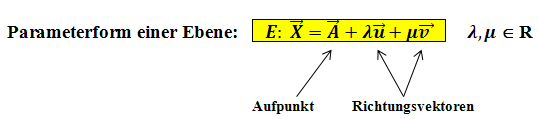
Damit die Richtungsvektoren wirklich eine Ebene aufspannen, dürfen sie keine Vielfachen voneinander sein;sie müssen also linear unabhängig bzw. nicht kollinear sein. Zur Erinnerung:Zwei Vektoren sind linear abhängig / kollinear, wenn sie Vielfache voneinander sind. Dann sind sie „parallel“ und spannen keine Ebene auf! (Genaueres dazu findest du im Kapitel Lineare Abhängigkeit)
So wie eine Gerade durch zwei Punkte eindeutig festgelegt ist, ist eine Ebene durch drei Punkte eindeutig bestimmt, wenn die Punkte nicht auf einer Geraden liegen. Drei Punkte, die auf einer Geraden liegen, legen nur diese Gerade fest, jedoch keine Ebene! Das kannst du dir ganz einfach mit Hilfe deiner Hände vorstellen:Nimm eine Hand und spreize drei Finger (am besten Daumen, Zeigefinger und Mittelfinger) so, dass z.B. ein Geodreieck oder deine Formelsammlung darauf liegen bleibt. An den Fingerspitzen denkst du dir die drei Punkte A, B und C. Das Geodreieck bzw. die Formelsammlung, je nachdem was du verwendest, stellt die Ebene dar. (Streng genommen eigentlich nur einen Ausschnitt der Ebene, denn eine Ebene geht ja in alle Richtungen weiter, sie hat schließlich keinen Rand.) Wenn die drei Punkte A, B und C nicht auf einer Gerade liegen, kann das Geodreieck auf den drei Fingerspitzen liegen bleiben. Dann ist durch diese drei Punkte eindeutig eine Ebene festgelegt. Das Geodreieck bzw. die Formelsammlung würde sofort herunter fallen, wenn die Punkte in einer geraden Linie hintereinander liegen würden. Dann wäre natürlich keine Ebene durch die drei Punkte festgelegt.
Ebenengleichungen in Parameterform aufstellen:
Eine Ebene kann nicht nur durch drei Punkte, die nicht auf einer Geraden liegen, bestimmt sein, sondern auch durch einen Punkt P und eine Gerade g, wobei P nicht auf g liegen darf. Durch zwei sich schneidende oder zwei parallele Geraden ist eine Ebene ebenfalls eindeutig festgelegt. Es kann außerdem eine Gerade g gegeben sein, die in der Ebene E liegt, und eine zur Ebene E parallele Gerade h. Auch so lässt sich eine Ebenengleichung aufstellen. Je nachdem, was angegeben ist, muss die Gleichung der Ebene E auf verschiedene Art und Weise ermittelt werden.
| Du kannst nun auswählen, mit welchen Angaben du eine Ebenengleichung in Parameterform aufstellen möchtest.
Ebene in Parameterform aufstellen mit folgenden Angaben: 1.Drei Punkte, die nicht auf einer Geraden liegen 2.Ein Punkt und eine Gerade,wobei der Punkt nicht auf der Geraden liegt 3.Zwei sich schneidende Geraden,die in der Ebene liegen sollen 4.Zwei parallele Geraden, die in der Ebene liegen sollen
|
