Hesse-Normalenform einer Ebene
Warum der Ausdruck 
im Nenner der HNF dies aussagt, soll nun erklärt werden:
Stell dir vor, die Konstante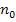 
hätte ein positives Vorzeichen. Dann ist 
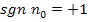. (sgn einer positiven Zahl ist immer gleich +1. Vergleiche oben!) Dann muss für den Ausdruck gelten: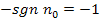 
Bei einer Konstante mit positivem Vorzeichen soll also durch die Zahl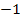 
geteilt werden, was dem Umdrehen aller Vorzeichen in der Koordinatenform entspricht.
Jetzt stellen wir uns vor, die Konstante 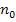hätte ein negatives Vorzeichen. Dann gilt 
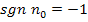. (sgn einer negativen Zahl ist immer gleich -1. Vergleiche oben!) Dann muss für den Ausdruck gelten: 
Bei einer Konstante mit negativem Vorzeichen soll also durch die Zahl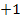 
geteilt werden, was nichts anderes bedeutet, als dass man die Vorzeichen lassen soll, wie sie sind, da eine Division durch die Zahl +1 nichts verändert.
Daher bedeutet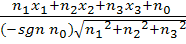 
nichts anderes, als dass die Koordinatenform einer Ebene durch den Betrag des Normalenvektors geteilt und die Vorzeichen der Koordinatenform umgedreht werden sollen, wenn die Konstante 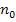positiv ist. Andernfalls bleiben die Vorzeichen in der Koordinatenform, wie sie sind, und die Koordinatenform wird nur durch den Betrag des Normalenvektors dividiert.
Nun stellt sich allerdings noch die Frage, was im Fall von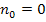 
passiert. Streng genommen ist die HNF für 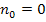gar nicht definiert, da der Nenner wegen sgn0 = 0 Null ergeben würde. Allerdings bedeutet 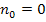, dass der Ursprung in der Ebene liegt. Dadurch zeigt jeder Normalenvektor weg vom Ursprung, egal ob die Vorzeichen umgedreht werden oder nicht. Daher ist die HNF in diesem Fall nicht eindeutig festgelegt.
Anwendungen der Hesse-Normalenform findest du in den Kapiteln:
Abstand:Punkt – Ebene (ohne Lotfußpunkt)
Abstand windschiefer Geraden (ohne Lotfußpunkte)
Winkelhalbierendenebenen
