Hesse-Normalenform einer Ebene
Signum-Funktion: f(x) = sgn x
Die Bezeichnung Signum-Funktion leitet sich vom lateinischen Wort signum = Zeichen bzw. Vorzeichen ab. Wie die Bezeichnung schon vermuten lässt, gibt sie im Prinzip das Vorzeichen einer Zahl an. Die Funktionsgleichung f(x) = sgn x ordnet aber jeder Zahl x nicht nur ihr nacktes Vorzeichen zu, sondern jeweils eine der drei Zahlen +1, -1 oder 0.
f(x) = 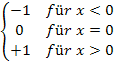
In Worten:
Jeder negativen Zahl x ordnet die Signum-Funktion den Wert -1 zu.
Ist x gleich Null, wird durch die Signum-Funktion wieder die Zahl Null zugeordnet
Jeder positiven Zahl x ordnet die Signum-Funktion den Wert +1 zu.
Die Signum-Funktion kann außerdem in der folgenden Form geschrieben werden:
f(x) = sgn x = 
.
Beispiele: sgn(-5) = -1
![]() sgn(+7) = +1
sgn(+7) = +1
![]() sgn(-2,47) = -1
sgn(-2,47) = -1
![]() sgn
sgn 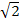 = +1
= +1
![]() sgn0 = 0
sgn0 = 0
Nun zurück zur HNF:In der vektoriellen Form der HNF 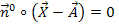 wird offensichtlich der Einheitsnormalenvektor
wird offensichtlich der Einheitsnormalenvektor 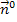 verwendet. Das ist leicht zu erkennen. Doch wird außerdem für die Orientierung des Einheitsnormalenvektors verlangt, dass gilt:
verwendet. Das ist leicht zu erkennen. Doch wird außerdem für die Orientierung des Einheitsnormalenvektors verlangt, dass gilt:![]()
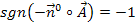
Was soll das aber bedeuten? Da das Ergebnis von sgn  gleich -1 sein soll, muss der Ausdruck
gleich -1 sein soll, muss der Ausdruck 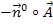 negativ sein. (sgn einer negativen Zahl ist -1, vergleiche oben!) Was bedeutet nun aber der Ausdruck
negativ sein. (sgn einer negativen Zahl ist -1, vergleiche oben!) Was bedeutet nun aber der Ausdruck 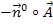 ? Der Ausdruck
? Der Ausdruck 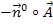 steht nur für die Konstante
steht nur für die Konstante 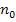 in der Koordinatenform der HNF.
in der Koordinatenform der HNF.

