Hesse-Normalenform einer Ebene

Geg.: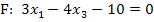   

Ausführlich könnte man auch schreiben:

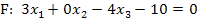
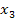So lässt sich der Normalenvektor ganz einfach an den Zahlen vor vor und ablesen:

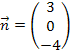
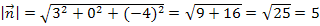
HNF: 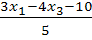   = 0

Zusammenfassung: Die HNF ist eine besondere Normalenform, die als Normalenvektor den Einheitsnormalenvektor verwendet, der so orientiert ist, dass er von der Ebene aus gesehen nicht zum Ursprung hin, sondern vom Ursprung weg zeigt. Siehe Abbildung! Die Koordinatenform der HNF wird gebildet, indem man bei der Koordinatenform der Ebene die Vorzeichen umdreht, wenn die Konstante positiv ist, und außerdem durch den Betrag des Normalenvektors teilt. Ist das Vorzeichen der Konstante bereits negativ, kann man die Koordinatenform der Ebene einfach abschreiben und durch den Betrag des Normalenvektors teilen

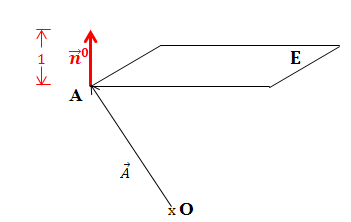
Abb. Darstellung einer Ebene in Hesse-Normalenform

In der Hesse-Normalenform hat der Normalenvektor den Betrag 1 und zeigt ausgehend von einem Ebenenpunkt A weg vom Ursprung. Da in dieser Abbildung der Ursprung unterhalb der Ebene E liegt, zeigt der Normalenvektor der HNF nach oben. (Wäre der Ursprung oberhalb der Ebene eingezeichnet worden, müsste der Normalenvektor der HNF nach unten zeigen.)

Nun soll die HNF allgemein in ihrer mathematisch korrekten Form gezeigt werden. So steht die Hesse-Normalenform meist in der Formelsammlung oder in den Schulbüchern. Leider wird ein Nichtmathematiker sie in dieser Form ohne weitere eingehende Erklärung kaum verstehen. (Keine Sorge, es wird unten noch alles genau erläutert! Schau dir die Formeln für die HNF einfach einmal an!)

HNF in vektorieller Form:

Orientierung von 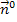so, dass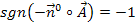  

HNF in Koordinatenform:

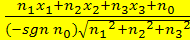
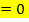
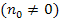
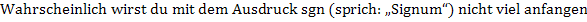können, da die sogenannte Signum-Funktion vermutlich im Unterricht nicht behandelt wurde. (Früher wurde sie manchmal in der 11. Klasse des Gymnasiums kurz besprochen, doch inzwischen wird sie kaum noch behandelt.) Daher soll die Signum-Funktion nun kurz erläutert werden.

---