Hesse-Normalenform einer Ebene
(Es gibt auch eine vektorielle Hesse-Normalenform;die brauchst du aber nicht.) Manche Lehrer schreiben die HNF auch folgendermaßen:
HNF: 
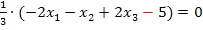
Das entspricht natürlich der oben gezeigten Form der HNF. Ob man durch 3 teilt oder ob man mit 
multipliziert, ist ja das Selbe. Entscheidend sind bei beiden Varianten der HNF allerdings die folgenden zwei Dinge:Das Vorzeichen der Konstanten ist negativ, es steht also ein Minus vor der 5, und der Normalenvektor ist ein Einheitsvektor. Dass in der HNF wirklich ein Einheitsnormalenvektor vorliegt, wird erst durch folgende Rechnung deutlich:
HNF: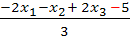 
HNF: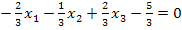 
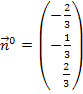
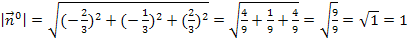
Der Betrag des Normalenvektors der HNF ist 1 und deshalb ist er wirklich ein Einheitsnormalenvektor.
Hier noch ein weiteres Beispiel:
2. Bsp.: Bilde die HNF der Ebene F!
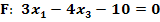
Lösung:
In diesem Beispiel ist das Vorzeichen der Konstante bereits passend, d.h. es steht ein Minus vor der Zahl 10. Die Orientierung des Normalenvektors ist also schon richtig. Wir können die Vorzeichen in der Koordinatenform lassen, wie sie sind. Es muss nur noch durch den Betrag des Normalenvektors geteilt werden. Daher berechnen wir vorab den Betrag des Normalenvektors.
