Hesse-Normalenform einer Ebene
Lösung:
Zuerst lesen wir den Normalenvektor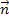 
aus der gegebenen Koordinatenform der Ebene E ab, d.h. wir nehmen einfach die Zahlen vor 
sowie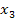 
und schreiben sie als Vektor übereinander.
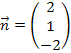
Dieser Normalenvektor ist noch kein Einheitsnormalenvektor;das erkennt man daran, dass sein Betrag nicht gleich 1 ist. (Wenn du nicht mehr weißt, wie man den Betrag eines Vektors bildet, gehe zu:Betrag eines Vektors)
Außerdem hat dieser Normalenvektor die falsche Orientierung, da das Vorzeichen der Konstante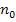 
in der Koordinatenform der Ebene positiv ist. Er schaut also zum Ursprung hin, weil vor der Konstante 5 ein Plus-Zeichen steht!
In der Hesse-Normalenform muss vor der Konstante 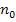ein Minus-Zeichen stehen, damit der Normalenvektor vom Ursprung wegschaut. Weil in der angegebenen Koordinatenform aber ein Plus-Zeichen vor der Konstante steht, müssen alle Vorzeichen der Koordinatenform umgedreht werden. Damit außerdem der Einheitsnormalenvektor entsteht, muss noch durch den Betrag des Normalenvektors dividiert werden.
Geg.: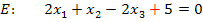 
HNF: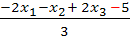 
Das ist schon die HNF in Koordinatenform der angegebenen Ebene E.
