Zueinander senkrechte (orthogonale) Geraden

2.    Bsp.: Gegeben ist die Gerade . Im Punkt P(2∣ soll das Lot errichtet werden. Ermittle durch Rechnung die Gleichung der Lotgeraden !

Hinweis:Ein Lot bzw. eine Lotgerade ist eine Gerade, die senkrecht steht auf der anderen Gerade! Es soll also die Gleichung einer Gerade ermittelt werden, die auf der angegebenen Gerade senkrecht steht. Der Punkt P muss dabei der Schnittpunkt der beiden Geraden sein, da das Lot in ihm errichtet werden soll. Dieser Punkt liegt also auf beiden Geraden!

Lösung:

Zuerst lösen wir die Geradengleichung nach y auf, damit deren Steigung abgelesen werden kann:

∣

∣

Nun berechnen wir die y-Koordinate des Punktes P. Da der Punkt P auch auf der Gerade liegt, kann die x-Koordinate von P in die Gleichung der Gerade eingesetzt werden, um die y-Koordinate von P zu berechnen.

P(2∣2)

Jetzt muss die Steigung der zu senkrechten Gerade ermittelt werden:

Das bedeutet, dass wir bei das Vorzeichen umdrehen und den Kehrwert bilden, also Zähler und Nenner vertauschen müssen, um zu erhalten.

Nun kennen wir die Steigung und die Koordinaten des Punktes P, der auch auf der Gerade liegt. Es muss also nur noch der y-Achsenabschnitt  der Gerade  berechnet werden.

Das kann entweder mit oder ohne Hilfe der „Punktsteigungsform“ einer Geraden geschehen.

·        Variante 1:Ohne „Punktsteigungsform“

Hast du die „Punktsteigungsform“ im Unterricht nicht gelernt, gehst du folgendermaßen vor:

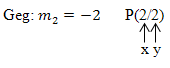
Setze ein in die allgemeine Geradengleichung y = mx+t

∣

Setze nun m und t in y = mx+t ein:   

·        Variante 2:Mit „Punktsteigungsform“

Hast du die „Punktsteigungsform“ im Unterricht gelernt, setzt du die Steigung und die Koordinaten von P(2/2) in die Punktsteigungsform ein.

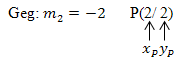
Setze ein in die Punktsteigungsform

Vereinfache die Gleichung                   

Wir erhalten die gesuchte Gerade 

Damit du dir besser vorstellen kannst, was du soeben berechnet hast, hier die Graphen der beiden Geraden im Koordinatensystem:

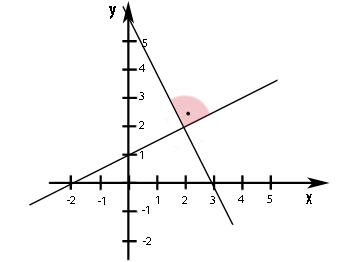
Abb.: Darstellung der Geraden  

---