Waagrechte und senkrechte Geraden
Eine waagrechte Gerade ist weder steigend noch fallend, ihre Steigung ist dahe m = 0. Setzt man m = 0 in die allgemeine Geradengleichung y = mx+t ein, erhält man die allgemeine Gleichung einer Waagrechten: y = 0x+t → y = t (y = Zahl)
1. Bsp.: f: y = 2
Die Funktionsgleichung y = 2 könnte auch ausführlicher in der Form y = 0x+2 geschrieben werden. Bei der Funktion f handelt es sich also um eine Waagrechte Gerade, da m = 0 ist. Sie schneidet die y-Achse im Punkt T(0; 2), da t =2 ist. Der Graph der Funktion f ist deshalb eine Parallele zur x-Achse im Abstand 2 nach oben verschoben. Siehe Abb. 8.43!
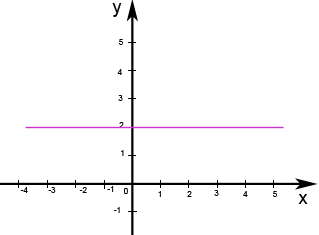
Abb. 8.43 Graph der Funktion f: y = 2
Solltest du Probleme haben, dir vorzustellen, dass y = 2 eine waagrechte Gerade beschreibt, versuche folgende Gedankenschritte nachzuvollziehen:
Betrachte den Graph der Funktion f in Abb. 8.43! Wähle einige Punkte mit einfach abzulesenden Koordinaten aus, die auf der Gerade liegen, und lies ihre Koordinaten ab! Beispielsweise: (1; 2), (2; 2), (3; 2), (4; 2) usw. Du kannst erkennen, dass die x-Koordinaten zwar variieren, aber die y-Koordinate immer y = 2 ist. Die Menge aller Punkte, deren x-Koordinaten alle beliebigen Werte annehmen können, aber deren y-Koordinate immer y = 2 ist, bildet die waagrechte Gerade, die in Abb. 8.43 zu sehen ist.
Es handelt sich eindeutig um eine Funktion, da jedem x genau ein y, nämlich y = 2 zugeordnet wird.
2. Bsp.: g: y = 0
Die Funktionsgleichung g: y = 0 lässt sich auch ausführlicher in der Form y =0x+0 schreiben. So kann man leichter erkennen, dass sowohl m = 0 als auch t = 0 ist. Es handelt sich wegen m = 0 um eine waagrechte Gerade, die außerdem wegen t = 0 durch den Ursprung verläuft. In anderen Worten: y = 0 ist die Gleichung der x-Achse. Die x-Achse stellt also selbst auch eine Funktion dar. Es wird ja jedem x-Wert genau ein y-Wert, nämlich y = 0 zugeordnet. Deshalb ist die x-Achse, wie auch jede andere waagrechte Gerade eine Funktion.
Senkrechte Geraden sind dagegen keine Funktionen, da einem x-Wert unendlich viele verschiedene y-Werte zugeordnet werden. Erinnere dich an die Definition einer Funktion: Eine Funktion ordnet jedem x genau ein y zu. Das ist bei senkrechten Geraden eindeutig nicht erfüllt. Daher sind senkrechte Geraden keine Funktionen. Trotzdem lässt sich auch eine senkrechte Gerade durch eine Gleichung beschreiben. Die Gleichung x = a, wobei a für eine konstante Zahl steht, beschreibt eine Parallele zur y-Achse im Abstand a.
3. Bsp.: h: x = 1
Die Gleichung x = 1 beschreibt eine Parallele zur y-Achse im Abstand 1, also eine senkrechte Gerade. Vergleiche dazu Abb. 8.44!
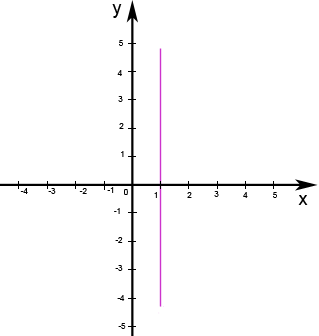
Abb. 8.44 Graph von h: x = 1
Solltest du Probleme haben, dir vorzustellen, dass x = 1 eine senkrechte Gerade beschreibt, versuche folgende Gedankenschritte nachzuvollziehen:
Betrachte den Graph der Funktion h in Abb. 8.44! Wähle einige Punkte mit einfach abzulesenden Koordinaten aus, die auf der Geraden h liegen, und lies ihre Koordinaten ab! Beispielsweise: (1; -1), (1; 0), (1; 1), (1; 2) usw. Du kannst erkennen, dass die y-Koordinaten zwar variieren, aber die x-Koordinate immer x = 1 ist. Die Menge aller Punkte, deren y-Koordinaten alle beliebigen Werte annehmen können, aber deren x-Koordinate immer x = 1 ist, bildet die senkrechte Gerade, die in Abb. 8.44 zu sehen ist.
Es handelt sich eindeutig um keine Funktion, da dem x-Wert x = 1 nicht genau ein y, sondern unendlich viele y-Werte zugeordnet werden.
4. Bsp.: k: x = 0
Dies ist die Gleichung der y-Achse, da alle Punkte, die auf der y-Achse liegen, die x-Koordinate x = 0 haben.

Merke dir die Gleichungen der Koordinatenachsen gut! Du wirst sie noch oft brauchen!
Achtung: Viele Schüler verwechseln die Gleichung der x-und der y-Achse!
Also merke dir gut: Zur x-Achse gehört die Gleichung y = 0 (und nicht x = 0!)
Zur y-Achse gehört die Gleichung x = 0 (und nicht y = 0!)

