Sich schneidende, parallele und identische Geraden im R∧2
Gegeben sind die beiden Geraden 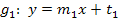 und
und 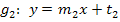 .
.
Es soll rechnerisch (also ohne Zeichnung) die Lage der beiden Geraden zueinander überprüft werden. Man soll also herausfinden, ob sich die Geraden schneiden, ob sie parallel oder identisch sind.
Merke:Zwei Geraden sind genau dann parallel, wenn sie die gleiche Steigung haben, aber zwei verschiedene y-Achsenabschnitte.
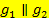 :
:![]()
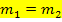
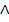

In Worten:Es sind zwei Geradengleichungen gegeben, die beide nach y aufgelöst sind. (Die Geraden liegen in ihrer expliziten Form bzw. Normalform vor.) Sind die Steigungen der beiden Geraden, also die Zahlen, die vor dem x stehen, gleich, die y-Achsenabschnitte, also die Konstanten (Zahlen ohne x) jedoch verschieden, dann liegen die beiden Geraden echt parallel zueinander. Mit „echt“ parallel ist gemeint, dass sie wirklich parallel und nicht etwa identisch (aufeinander liegend) sind.
Die Geraden 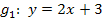 und
und 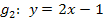 haben beide die gleiche Steigung
haben beide die gleiche Steigung![]()
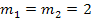 ,aber die unterschiedlichen y-Achsenabschnitte
,aber die unterschiedlichen y-Achsenabschnitte 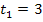 und
und 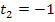 . Daher sind diese beiden Geraden (echt) parallel.
. Daher sind diese beiden Geraden (echt) parallel.
Identische Geraden haben nicht nur die gleiche Steigung, sondern auch den gleichen y-Achsenabschnitt.
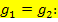
![]()
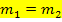
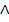
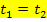
Die Geraden 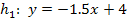 und
und 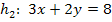 sind identisch, was jedoch auf den ersten Blick nicht erkennbar ist. Um die Lagebeziehung der beiden Geraden überprüfen zu können, müssen beide Geraden nach y aufgelöst sein. Die Gerade
sind identisch, was jedoch auf den ersten Blick nicht erkennbar ist. Um die Lagebeziehung der beiden Geraden überprüfen zu können, müssen beide Geraden nach y aufgelöst sein. Die Gerade 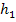 ist bereits nach y aufgelöst, die Gerade
ist bereits nach y aufgelöst, die Gerade 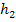 aber noch nicht. Deshalb muss
aber noch nicht. Deshalb muss 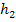 noch nach y aufgelöst werden. Erst dann können die Steigungen und die y-Achsenabschnitte abgelesen werden.
noch nach y aufgelöst werden. Erst dann können die Steigungen und die y-Achsenabschnitte abgelesen werden.
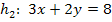 |
∣ 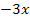 |
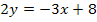 |
∣ 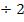 |
(Vorsicht:Sowohl die Zahl vor dem x, hier -3, als auch die Zahl dahinter, hier +8, müssen beide jeweils durch 2 geteilt werden!)
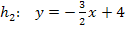
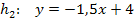
![]() vgl.:
vgl.: 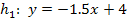
Nun sieht man sofort, dass die beiden Geraden 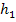 und
und 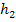 identisch sind, da die Steigung und der y-Achsenabschnitt beider Geraden gleich ist.
identisch sind, da die Steigung und der y-Achsenabschnitt beider Geraden gleich ist. 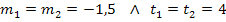
Haben zwei Geraden dagegen unterschiedliche Steigungen, schneiden sie sich. (Das hat nichts mit den y-Achsenabschnitten zu tun! Die y-Achsenabschnitte können gleich sein oder verschieden.)
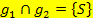
![]()
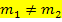
Die Geraden 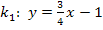 und
und 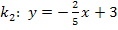 schneiden sich, da sie unterschiedliche Steigungen haben. Die Steigung (Zahl vor dem x) der Gerade
schneiden sich, da sie unterschiedliche Steigungen haben. Die Steigung (Zahl vor dem x) der Gerade 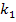 ist
ist 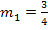 . Die Steigung der Gerade
. Die Steigung der Gerade 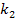 ist
ist 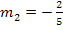 . Die Steigungen sind nicht gleich, daher müssen sich die beiden Geraden schneiden.
. Die Steigungen sind nicht gleich, daher müssen sich die beiden Geraden schneiden.
Haben zwei Geraden unterschiedliche Steigungen, aber den gleichen y-Achsenabschnitt, schneiden sie sich genau in ihrem Schnittpunkt mit der y-Achse T(0∣t).
Die Geraden 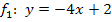 und
und 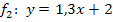 haben verschiedene Steigungen
haben verschiedene Steigungen 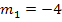 und
und 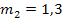 . Deshalb schneiden sie sich. Der Schnittpunkt liegt genau auf der y-Achse, weil beide Geraden denselben y-Achsenabschnitt
. Deshalb schneiden sie sich. Der Schnittpunkt liegt genau auf der y-Achse, weil beide Geraden denselben y-Achsenabschnitt 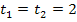 haben. Der Schnittpunkt hat daher die Koordinaten T(0∣2).
haben. Der Schnittpunkt hat daher die Koordinaten T(0∣2).
| Lagebeziehungen zweier Geraden zueinander
(Zusammenfassung):
Gegeben sind die beiden Geraden |
|||||||||
|
![]()
![]()
1. Bsp.: Welche der folgenden Geraden sind parallel zueinander?
(Löse die Aufgabe zuerst ohne Verwendung einer Zeichnung! Kontrolliere deine Ergebnisse dann durch Zeichnung im Koordinatensystem!)
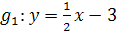
![]()
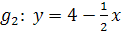
![]()
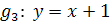
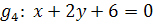
![]()
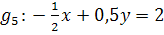
![]()
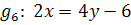
Zwei Geraden sind genau dann parallel zueinander, wenn sie die gleiche Steigung, aber verschiedene y-Achsenabschnitte haben. Um herauszufinden, welche der Geraden parallel zueinander sind, müssen daher bei jeder der gegebenen Geraden die Steigung m und der y-Achsenabschnitt t ermittelt werden.
Die Geraden 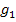 bis
bis 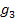 sind bereits nach y aufgelöst;bei diesen Geradengleichungen lässt sich die Steigung m und der y-Achsenabschnitt t sofort ablesen.
sind bereits nach y aufgelöst;bei diesen Geradengleichungen lässt sich die Steigung m und der y-Achsenabschnitt t sofort ablesen.
Achtung:Bei Gerade 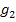 stimmt die „Reihenfolge“ noch nicht! Die Steigung m ist nicht immer die vordere Zahl, sondern die Zahl vor dem x! Am besten ist es, die Gleichung zu ordnen:Zuerst „die Zahl mit x“, dann erst „die Zahl ohne x“! (Vorzeichen dabei natürlich „mitnehmen“)
stimmt die „Reihenfolge“ noch nicht! Die Steigung m ist nicht immer die vordere Zahl, sondern die Zahl vor dem x! Am besten ist es, die Gleichung zu ordnen:Zuerst „die Zahl mit x“, dann erst „die Zahl ohne x“! (Vorzeichen dabei natürlich „mitnehmen“) 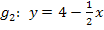
![]()
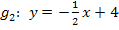
Bei Gerade 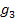 steht keine Zahl vor dem x, d.h. aber nicht, dass die Steigung m=0 ist, sondern dass m=1, weil x dasselbe wie 1x ist.
steht keine Zahl vor dem x, d.h. aber nicht, dass die Steigung m=0 ist, sondern dass m=1, weil x dasselbe wie 1x ist.
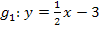 |
Steigung 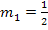 |
y-Achsenabschnitt 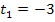 |
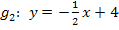 |
Steigung 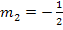 |
y-Achsenabschnitt 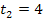 |
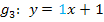 |
Steigung 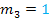 |
y-Achsenabschnitt 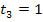 |
Bei den Geraden 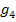 bis
bis 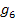 ist das nicht so einfach;diese Geradengleichungen müssen erst nach y aufgelöst werden, bevor m und t abgelesen werden können.
ist das nicht so einfach;diese Geradengleichungen müssen erst nach y aufgelöst werden, bevor m und t abgelesen werden können.
Vorsicht:Ist eine Geradengleichung noch nicht nach y aufgelöst, stellt die Zahl vor dem x nicht die Steigung m dar! So könnte man glauben, dass die Geraden 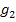 und
und 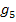 parallel sind, weil in beiden Gleichungen vor dem x die Zahl
parallel sind, weil in beiden Gleichungen vor dem x die Zahl 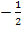 steht. Das ist aber falsch! Die Geraden
steht. Das ist aber falsch! Die Geraden 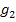 und
und 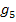 sind nicht parallel, was man deutlich erkennt, wenn auch
sind nicht parallel, was man deutlich erkennt, wenn auch 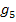 nach y aufgelöst wurde. (Vergleiche unten!) Entsprechendes gilt für die Geraden
nach y aufgelöst wurde. (Vergleiche unten!) Entsprechendes gilt für die Geraden 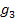 und
und 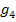 . Auch sie sind nicht parallel, obwohl die Zahlen vor dem x in der Angabe gleich sind. Wie bereits erwähnt, muss
. Auch sie sind nicht parallel, obwohl die Zahlen vor dem x in der Angabe gleich sind. Wie bereits erwähnt, muss 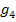 erst noch nach y aufgelöst werden, bevor man die Steigung m korrekt ablesen kann.
erst noch nach y aufgelöst werden, bevor man die Steigung m korrekt ablesen kann.
Löse daher immer zuerst nach y auf, bevor du m und t abliest! (Außer die Gerade ist bereits nach y aufgelöst;dann kann man sich das Auflösen natürlich schenken.)
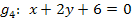 |
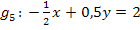 |
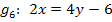 |
Nun lösen wir nacheinander die Geradengleichungen 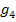 bis
bis 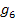 nach y auf und lesen dann jeweils die Steigung und den y-Achsenabschnitt ab:
nach y auf und lesen dann jeweils die Steigung und den y-Achsenabschnitt ab:
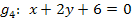 |
∣ 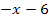 |
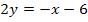 |
∣ 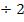 |
(Vorsicht:Sowohl die Zahl vor dem x, hier -1, als auch die Zahl dahinter, hier -6, müssen beide jeweils durch 2 geteilt werden!)
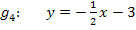
![]() Steigung
Steigung 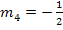
![]() y-Achsenabschnitt
y-Achsenabschnitt 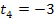
—————————————————————————————————————–
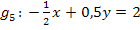 |
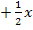 |
|
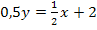 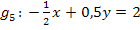 |
∣ 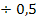 |
(Hinweis:„Geteilt durch 0,5“ entspricht „geteilt durch  “. Durch einen Bruch wird “. Durch einen Bruch wird
dividiert, indem man mit dem Kehrwert multipliziert, also hier mit |
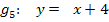 |
||
|
|
Steigung |
y-Achsenabschnitt 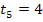 |
——————————————————————————————————————-
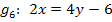
![]() ∣
∣ 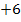
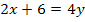
![]() ∣
∣ 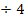
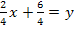
![]() (Kürzen nicht vergessen!)
(Kürzen nicht vergessen!)
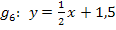
![]() Steigung
Steigung 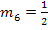
![]() y-Achsenabschnitt
y-Achsenabschnitt 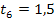
Der Übersicht wegen, hier noch einmal alle Geraden (nach y aufgelöst) mit ihrer Steigung m und ihrem y-Achsenabschnitt t:
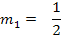 |
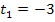 |
|
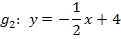 |
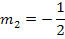 |
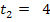 |
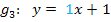 |
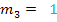 |
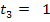 |
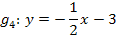 |
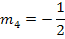 |
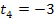 |
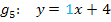 |
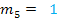 |
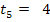 |
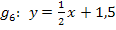 |
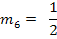 |
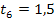 |
Man erkennt, dass die Geraden 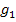 und
und 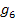 die gleiche Steigung
die gleiche Steigung 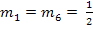 haben, aber unterschiedliche y-Achsenabschnitte
haben, aber unterschiedliche y-Achsenabschnitte 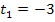 und
und 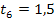 . Deshalb sind die Geraden
. Deshalb sind die Geraden 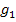 und
und 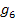 parallel.
parallel.
Die Geraden 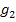 und
und 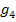 sind ebenfalls zueinander parallel, da sie die gleichen Steigungen
sind ebenfalls zueinander parallel, da sie die gleichen Steigungen 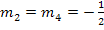 haben, aber unterschiedliche y-Achsenabschnitte
haben, aber unterschiedliche y-Achsenabschnitte 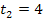 und
und 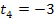 .
.
Die Geraden 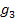 und
und 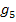 haben beide die Steigung
haben beide die Steigung 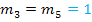 , jedoch unterschiedliche y-Achsenabschnitte
, jedoch unterschiedliche y-Achsenabschnitte 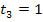 und
und 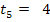 . Daher sind auch
. Daher sind auch 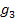 und
und 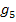 zueinander parallel.
zueinander parallel.
In Abbildung 8.51 sind diese Geraden im Koordinatensystem dargestellt.
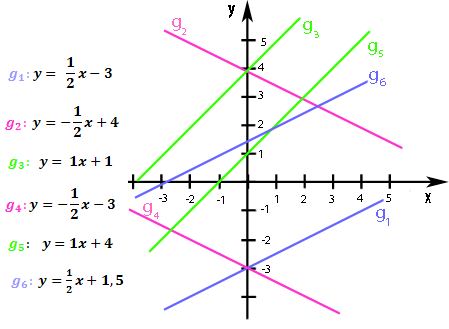
Abb. 8.51
2. Bsp.: Ermittle durch Rechnung die Gleichung der Gerade g durch den Punkt P(3∣0,5), die parallel zur Geraden 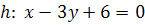 verläuft.
verläuft.
Zwei Geraden sind parallel zueinander, wenn sie die gleiche Steigung haben. Die Gerade g muss also die gleiche Steigung wie die Gerade h haben: 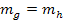
Um die Steigung der Geraden h zu ermitteln, muss die Gleichung von h nach y aufgelöst werden.
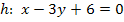
![]() ∣
∣ 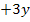
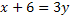
![]() ∣
∣ 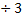
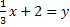
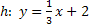
Nun kann die Steigung der Geraden h abgelesen werden: 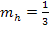
Wegen 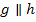 gilt:
gilt: 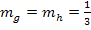
Nun ist die Steigung der Geraden g bekannt. Außerdem ist der Geradenpunkt P(3∣0,5) gegeben. Damit kann der y-Achsenabschnitt t der Geraden g berechnet werden.
Dafür gibt es zwei Methoden:Die erste Methode verwendest du, wenn du die sogenannte „Punktsteigungsform“ einer Geraden nicht im Unterricht gelernt hast. Gehst du auf ein Gymnasium, solltest du auf jeden Fall diese Methode benützen.
Schüler einer Realschule können aber auch die zweite Methode mit der „Punktsteigungsform“ einer Geraden verwenden;die Formel der Punktsteigungsform findest du in der mathematischen Formelsammlung für Realschulen in Bayern.
1. Methode: Ohne „Punktsteigungsform“
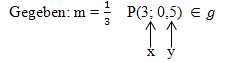
Allgemeine Geradengleichung: 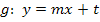
m und die Koordinaten von P für x und y einsetzen:
![]()
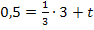
Nach t auflösen:![]()
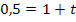
![]() ∣
∣ 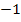
![]()
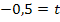
![]()
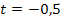
m und t einsetzen in  ergibt:
ergibt: 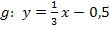
2. Methode: Mit der „Punktsteigungsform“ einer Geraden
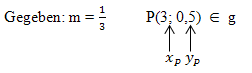
Punkt-Steigungsform: 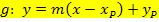 Siehe Formelsammlung (Realschule)!
Siehe Formelsammlung (Realschule)!
Einsetzen von m und P: 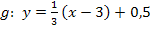
Vereinfachen: 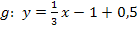
![]()
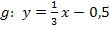

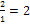 multipliziert.)
multipliziert.)