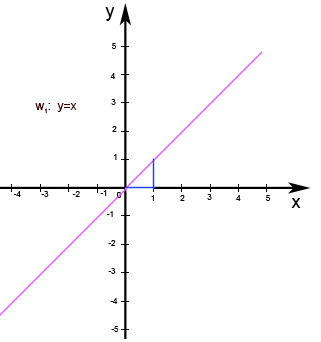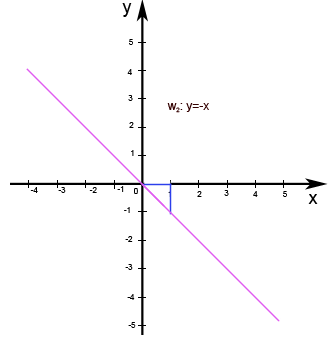Methode: Gerade mit Hilfe der Steigung m und des y-Achsenabschnitts t zeichnen
–[endif]–>
3. Bsp.: Zeichne die Geraden w1: y=x und w2: y=-x mit Hilfe des y-Achsenabschnitts eines Steigungsdreiecks in ein Koordinatensystem! Beschreibe die besondere Lage dieser beiden Geraden!
Die Gerade w1: y=x und kann auch ausführlich geschrieben werden in der Form: w1: y=1x+0
So kann man m und t leicht ablesen: m = 1 = 
Wegen t = 0 verläuft die Geradew1 durch den Ursprung, von dort geht man 1 nach rechts und 1 nach oben (m>0 ), um das Steigungsdreieck zu zeichnen.
Vergleiche Abb. 8.45! Es handelt sich bei der Gerade w1: y=x um die Winkelhalbierende durch den I. und III. Quadranten, d.h. um die steigende Winkelhalbierende.
Die Gerade w2: y=-x kann auch ausführlich geschrieben werden in der Form: w1: y=1x+0
So kann man m und t leicht ablesen: m = 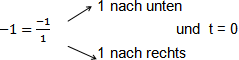
Wegen t = 0 verläuft die Gerade w2 ebenfalls durch den Ursprung, von dort geht man 1 nach rechts und 1 nach unten (m<0 ), um das Steigungsdreieck zu zeichnen.
Vergleiche Abb. 8.45! Es handelt sich bei der Gerade w2: y=-x um die Winkelhalbierende durch den II. und IV. Quadranten, d.h. um die fallende Winkelhalbierende.