Methode: Gerade mit Hilfe der Steigung m und des y-Achsenabschnitts t zeichnen
Von diesem Punkt aus zeichnet man dann das Steigungsdreieck:
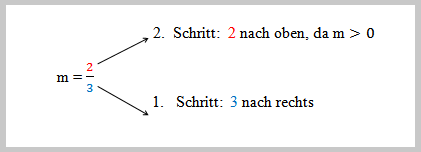
Vom Schnittpunkt mit der y-Achse aus geht man 3 cm nach rechts, dann 2cm nach oben (oder 3 Kästchen nach rechts und 2 Kästchen nach oben) und markiert diesen Punkt. Man muss den Zähler nach oben gehen, da die Steigung m positiv ist. Ob das ganze Steigungsdreieck eingezeichnet wird oder nur der Punkt markiert wird, bleibt jedem selbst überlassen. Für den Anfang wollen wir das Steigungsdreieck noch einzeichnen, später wird es dann allerdings weggelassen.
Hinweis: Man hätte stattdessen auch 3 nach links und 2 nach unten gehen können.
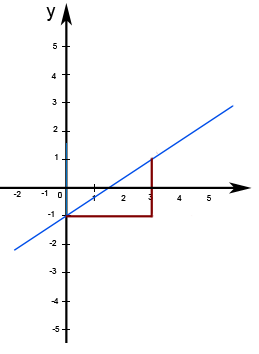
Abb. 8.41 Graph der Funktion
2. Bsp.: Zeichne den Graph der Funktion 
mit Hilfe eines Steigungsdreiecks und des y-Achsenabschnitts!
Diese Funktion ist noch nicht nach y aufgelöst, sie liegt also noch nicht in ihrer expliziten Form (= Normalform) vor. Wir müssen daher die Funktionsgleichung erst noch nach y auflösen, damit m und t abgelesen werden können.
Anmerkung:
Lineare Funktionen können in verschiedenen Formen vorliegen:
Explizite Form (= Normalform) einer Geraden: y=mx+t
Implizite Form einer Geraden: ax+by+c=0 , mit b≠0
Die Bezeichnung „explizite Form“ leitet sich vom lateinischen Wort explicare (= erklären) ab. Diese Form „erklärt“ praktisch, wie man die Gerade mit Hilfe der Steigung m und des y-Achsenabschnitts t zeichnen kann, da sich m und t direkt ablesen lassen.
Die Bezeichnung „implizite Form“ leitet sich vom lateinischen Wort implicare (= einschließen) ab. Die Steigung m und der y-Achsenabschnitt t lassen sich nicht direkt ablesen, da die Funktionsgleichung noch nicht nach y aufgelöst ist. Die Information ist also zwar „eingeschlossen“, aber nicht sofort ablesbar. Sie muss erst „ausgepackt“ werden, d.h. die Gleichung muss nach y aufgelöst, also in die explizite Form umgerechnet werden. Daher darf der Koeffizient b auch nicht gleich Null sein, sonst würde y herausfallen und es würde keine Funktion mehr vorliegen.
Umwandlung der expliziten in die implizite Form der Gerade: → Auflösen nach y
∣
∣ 
(Achtung: Teile sowohl -4x als auch +6 durch 3!
