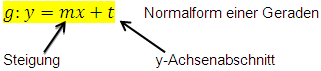Methode: Gerade mit Hilfe der Steigung m und des y-Achsenabschnitts t zeichnen
Ist eine Funktion nach y aufgelöst, liegt sie in ihrer Normalform bzw. expliziten Form vor. Wie bereits oben erklärt, handelt es sich um eine lineare Funktion, d.h. eine schräge oder waagrechte Gerade, wenn die Funktionsgleichung auf die Form y = mx+t gebracht werden kann.
Die Zahl vor dem x nennt man die Steigung m; die Konstante („Zahl ohne x“) nennt man den y-Achsenabschnitt t.
Die Bezeichnung y-Achsenabschnitt kommt daher, dass die Gerade die y-Achse immer im Punkt T(0; t) schneidet. Um eine Gerade mit Hilfe von m und t zu zeichnen, geht man also zuerst vom Ursprung um t auf der y-Achse nach oben (wenn t >0 ) bzw. nach unten (wenn t<0 ) und markiert diesen Punkt.
Anmerkung: Obwohl in der allgemeinen Geradengleichung y = mx+t ein Plus-Zeichen vor dem t steht, kann t selbst sowohl positiv als auch negativ sein. Ist t positiv, geht man auf der y-Achse um t nach oben, um den Schnittpunkt mit der y-Achse einzuzeichnen. Ist t dagegen negativ, geht man auf der y-Achse nach unten. Ist t = 0 (d.h. die Konstante/ Zahl ohne x fehlt) verläuft die Gerade durch den Ursprung. Eine Ursprungsgerade hat daher die allgemeine Form y = mx.
Vom Schnittpunkt mit der y-Achse ausgehend zeichnet man dann das sogenannte Steigungsdreieck. Das Steigungsdreieck erhält man, indem man sich die Steigung m als Bruch denkt: Den Nenner geht man am besten immer nach rechts, den Zähler nach oben, wenn m positiv ist, bzw. nach unten, wenn m negativ ist. Ist m eine ganze Zahl, nimmt man als Nenner die Zahl 1: z.B. m = 2 =![]()

Anmerkung:
Es ist empfehlenswert, zuerst den Nenner immer nach rechts (1. Schritt) und dann bei positivem m den Zähler nach oben bzw. bei negativem m nach unten (2. Schritt) zu gehen. 1. und 2. Schritt könnten von der Reihenfolge auch vertauscht werden. Entscheidend ist allerdings, dass sich der Nenner immer auf die x-Achse, der Zähler dagegen immer auf die y-Achse bezieht.