Lineare Funktionen in der Form g: y=mx+t

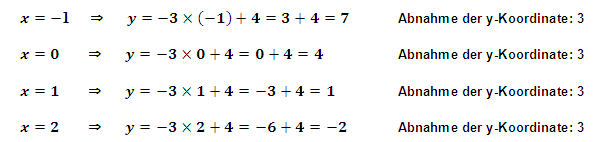
Wie erwartet nimmt die y-Koordinate jeweils um 3 ab, wenn die x-Koordinate um 1 vergrößert wird. Man könnte diese Rechnung ewig fortsetzen: Wenn x um 1 vergrößert wird, verkleinert sich y in diesem Beispiel immer  gleichmäßig um 3.

Der Graph der Funktion y = -3x+4 kann mit Hilfe der oben berechneten Punkte und gezeichnet werden. Um von einem Punkt zum nächsten zu kommen, geht man immer 1 nach rechts und 3 nach unten. Der Graph ist, wie erwartet eine Gerade.

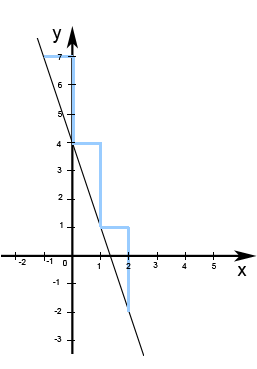
Abb. 8.40 Graph der Funktion y = -3x+4

Das Entscheidende ist, dass die Zu- bzw. Abnahme des y-Werts gleichmäßig ist, so dass für m ein gleichmäßig steigender  bzw. für  m  ein gleichmäßig fallender Graph, also eine steigende oder fallende Gerade, entsteht.

Nun bleibt noch der Fall m = 0:

Setzt man in die allgemeinen Geradengleichung y = mx+t für m die Zahl 0 ein, so erhält man:  Diese Funktion enthält kein x mehr, daher ist der y-Wert immer konstant t. Die Punkte, die auf der Funktion y = t liegen, haben also – egal bei welchem x-Wert – immer denselben y-Wert, nämlich t. Stell dir z.B. die Punkte … vor! Sie liegen alle auf einer Gerade, die im Abstand t parallel zur x-Achse verläuft. Es handelt sich beim Graph der Funktion y = t um eine waagrechte Gerade. Wenn du dir das nicht so richtig vorstellen kannst, weil t keine konkrete Zahl ist, hilft es sich für t eine bestimmte Zahl zu denken. Beispielsweise t = 2, die Gerade y = 2 liegt im Abstand 2 parallel zur x-Achse.

---