Variante: Aus einer Zeichnung ablesen
Geht man nach links und dann nach oben, ist m negativ.
Beim Steigungsdreieck nach links zu gehen, ist nicht empfehlenswert! Wenn irgend möglich gehst du besser immer nach rechts!
Nachdem man die Steigung m aus der Zeichnung abgelesen hat, muss noch der y-Achsenabschnitt t ermittelt werden. Da der Schnittpunkt mit der y-Achse nicht deutlich ablesbar ist, kann t nicht einfach abgelesen werden. Man muss t berechnen:
Dazu setzt man für x und y die Koordinaten eines Geradenpunkts, also entweder die Koordinaten von P1 oder die von P2 und die bereits bekannte Steigung m in die allgemeine Geradengleichung y = mx+t ein und löst dann nach t auf.
Genau genommen kann man ohne deutlich ablesbaren y-Achsenschnittpunkt die Gleichung der Geraden nicht einfach ablesen; t muss berechnet werden. Daher handelt es sich hier schon um einen Übergang zur rechnerischen Ermittlung der Geradengleichung. (Vergleiche dazu auch 2. Variante!)
Bsp.: In Abb. 8.48 a bis d sind die Graphen der Geraden h1 bis h4 dargestellt. Ermittle die Gleichungen der Geraden bis mit Hilfe der Zeichnung!
Anleitung: Zeichne die unten dargestellten Geraden mit Hilfe der klar ablesbaren Punkte auf kariertes Papier in getrennte Koordinatensysteme! Dann zeichnest du jeweils das Steigungsdreieck zu jeder Gerade und liest die Steigung m direkt aus der Zeichnung ab! Dann kannst du t berechnen.
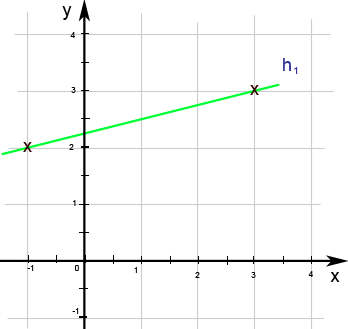
Abb. 8.48a
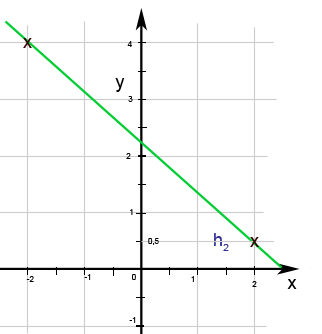
Abb. 8.48b
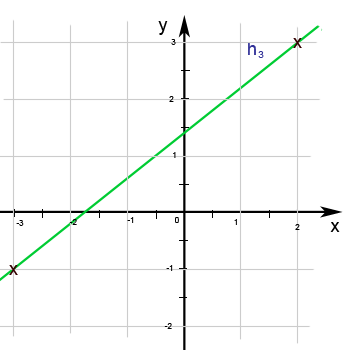
Abb. 8.48c
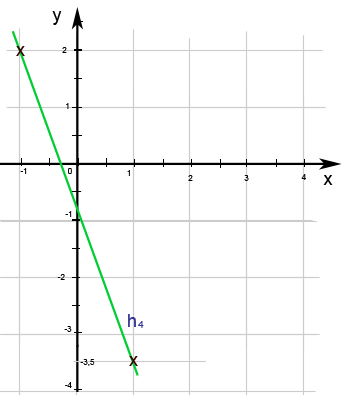
Abb.

