Variante: Aus einer Zeichnung ablesen
8.46c ist die Gerade dargestellt. Der Schnittpunkt mit der y-Achse hat die Koordinaten T(0; -1,5). Deshalb gilt: t = -1,5 In Abb. 8.47c kannst du die Gerade mit ihrem Steigungsdreieck sehen. Um von P(-4; -3) zum Punkt T(0; -1,5) zu gelangen, müsste man 4 cm nach rechts und 1,5 cm nach oben gehen. Besser ist es in diesem Fall jedoch mit Kästchen zu zählen: Also 8 Kästchen nach rechts und 3 Kästchen nach oben. Da hier nach oben gegangen wurde, ist die Steigung m positiv.
Durch die Verwendung von Kästchen statt cm kann verhindert werden, dass im Zähler von m eine Dezimalzahl/Kommazahl steht. Ein Bruch mit Dezimalbruch im Zähler oder Nenner sollte vermieden werden!
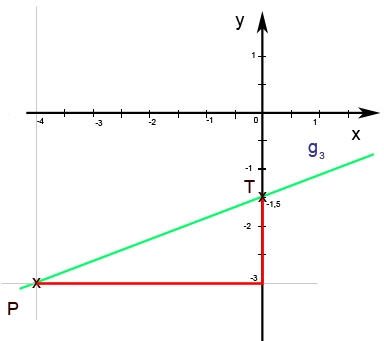
Abb. 8.47c
Was im Steigungsdreieck nach rechts gegangen wird, steht im Nenner. In diesem Fall musste man ja 8 Kästchen nach rechts gehen, daher steht im Nenner von m die Zahl 8.
Was im Steigungsdreieck nach oben (oder unten) gegangen wird, steht im Zähler. In diesem Fall musste man ja 3 Kästchen nach oben gehen, daher steht im Zähler von m die Zahl 3.
Die Steigung m der Geraden g3 lautet deshalb: m = ![]()
Nun können wir die Gleichung von angeben: In Abb. 8.46d ist der Graph der Gerade dargestellt. Da der Schnittpunkt mit der y-Achse bei T(0; -0,5) liegt, gilt für den y-Achsenabschnitt: t = -0,5 Um das Steigungsdreieck einzuzeichnen, gehen wir vom Punkt P(-3; 2,5) zum Schnittpunkt mit der y-Achse T(0; -0,5) und nicht anders herum von T zu P, da P links von T liegt. Vergleiche Abb. 8.47d!
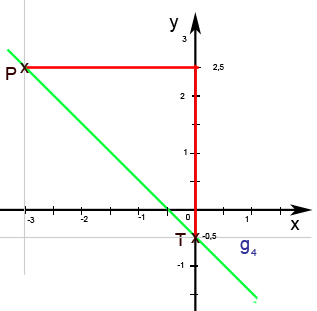
Abb.

